第一章 三角形的初步知识复习（一）
复习目标；
回顾三角形的内角关系，内角与外角的关系，三边关系和三角形中主要线段的性质，并能熟练运用这些性质解决有关的计算，提高学生探究、观察、猜想、说理等能力，改善沟通、表达及合作的技巧。
一、知识要点
1、三角形按内角的大小分为三类： 、 、 。
2、三角形内角和是 ，直角三角形的两锐角 。
3、三角形的内角与外角的关系：三角形的一个外角等于和它 的两个内角的和。
4、三角形的三边关系：三角形任何两边的和 第三边；三角形任何两边的差 第三边。
5、三角形中的主要线段：三角形的中线、三角形的角平分线和三角形的高。
三角形的三条角平分线交于 ，三条中线交于 ，三条高所在的直线交于 。三角形的角平分线、中线、高线、中垂线都是线段。
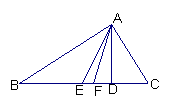6、如图，在△ABC中，
（1）AE是中线，那么BE＝ ＝ ，
BC＝ BD＝ DC；
（2）AF是角平分线，那么∠BAF＝ ＝ ，
∠BAC＝ ∠BAF＝ ∠FAC；
（3）AD是BC边上的高线，那么∠ADB＝∠ADC＝ °，AD BC。
二、课内练习
1、看图识别
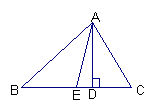如图:在锐角△ABC中,AD⊥BC于D,E是BC上一点,连接AE.
(1)锐角三角形有_____个
(2)钝角三角形有_____个
(3)直角三角形有_____个
2、计算判别
根据下列条件判断它们各是什么三角形？
（1）两个内角是70°和30°（ ）
（2）三个内角的度数是1:2:3（ ）
（3）△ABC中∠A-∠B=90°（ ）
3、如图，△ABE的外角是 ，∠AEB是 的外角，
∠ADC是 的内角，又是 的外角，若∠B=40°，
∠BAE=30°，则∠AEB= ，∠EAD= 。
4、判断下列各组线段中，哪些能组成三角形？哪些不能组成三角形？并说明理由。
（1）3，4，5； （2）8，7，15；
（3）3a，4a，5a； （4）k+1，2k，k+1。
5、已知一个三角形的三边长为3，8，x，则x的取值范围是 ，该三角形周长的取值范围是 ，若x是奇数，则x是 。
6、三角形的三边长为a,b,c, 已知a>b，化简代数式 b – a + a – b – c
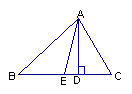
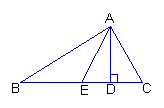
7、如图,在△ABC中,AE是边BC上的中线.
（1）已知AB=4,AE=3,BC=5, 求△ABE的周长；
（2）已知AB=4，AC=3，求△ABE和△ACE的周长的差；
（3）在（2）中△ABE和△ACE的面积有何关系？
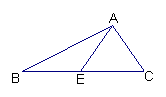
8、已知△ABC中，∠B=45°，∠C=75°，AD是BC边上的高，AE是∠BAC的平分线，求∠AED，∠DAE的度数。
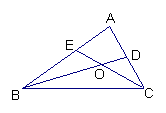9、如图，在△ABC中，两条角平分线BD和CE相交于点O，若∠BOC=120°，那么∠A的度数是
.
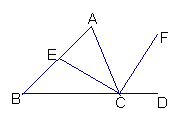
10、如图,CE,CF分别是△ABC的内角平分线和外角平分线,求∠ECF的度数.
1. 如图,在△ABC中, ∠ACB=90°,CD是斜边上的高,CE是△ABC的角平分线.已知∠AEB=105°,分别求∠BEC, ∠ECD的度数.
三角形的初步知识复习（二）
6、两个能够完全重合的图形称为 ；
全等三角形的对应边 ，对应角 。
7、三角形全等的条件：
①三边对应相等的两个三角形全等，简写成 或___
②两角和它们的夹边对应相等的两个三角形全等，
简写成 或 ____
③两角和其中一角的对边对应相等的两个三角形全等，
简写成 或_____
④两边和它们的夹角对应相等的两个三角形全等，
简写成 或 _____
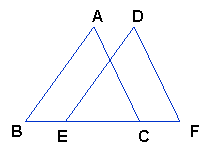
如图,已知△ABC≌△DEF.请找出他们的
对应边和对应角