第七章 三角形期中考复习题
一 选择题
1、以下列各组长度的线段为边，能构成三角形的是：
A．7cm，5cm，12cm B．6cm，8cm，15cm
C．4cm，6cm，5cm D．8cm，4cm，3cm
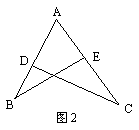
2、如图2，已知∠B＝∠C，则∠ADC与∠AEB的大小关系是：
A、∠ADC＞∠AEB B、∠ADC＜∠AEB
C、∠ADC＝∠AEB D、大小关系不能确定
3、一个多边形的内角和比它的外角和的2倍还大180°，这个多边形的边数为：
A．7 B．8 C．9 D．10
4、用一批完全相同的多边形地砖铺地面，不能进行镶嵌的是( )
A、正三角形 B、正方形 C、正八边形 D、正六边形
5、已知线段a、b、c，有a＞b＞c，则组成三角形必须满足的条件是( )
A.a+b>c B.b+c>a C.c+a>b D.a-b>c
6、能把三角形的面积平分的是( )
A.三角形的角平分线 B.三角形的高 C.三角形的中线 D.以上都不对
7、下列图形中能够用来作平面镶嵌的是（ ）
A、正八边形 B、正七边形 C、正六边形 D、正五边形
8、△ABC中，三边长分别为6,7，x，则x的取值范围为（ ）。
A、2＜x＜12 B、1＜x＜13 C、6＜x＜7 D、无法确定
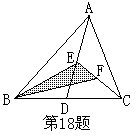
9、如图△ABC中已知D、E、F分别为BC、AD、CE的中点，且S△ABC＝4cm2，则S阴影的值为（ ）A、2cm2 B、
cm2 C、
cm 2 D、1cm2
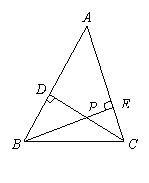
10、如图，在锐角△ABC中，CD、BE分别是AB、AC边上的高，
且相交于一点P，若∠A=50°，则∠BPC的度数是（ ）
A．150° B．130° C．120° D．100°
11、中华人民共和国国旗上的五角星，它的五个锐角的度数和是（ ）
A、500 B、100 0 C、180 0 D、 200 0
12、在
ABC中，三个内角满足∠B－∠A=∠C－∠B，则∠B等于（ ）
A、70° B、60° C、90° D、120°
13、在锐角三角形中，最大内角的取值范围是（ ）
A、0°＜
＜90°
B、60°＜＜180° C、60°＜＜90° D、60°≤＜90
14、给出下列命题：①三条线段组成的图形叫三角形 ②三角形相邻两边组成的角叫三角形的内角 ③三角形的角平分线是射线 ④三角形的高所在的直线交于一点，这一点不在三角形内就在三角形外 ⑤任何一个三角形都有三条高、三条中线、三条角平分线 ⑥三角形的三条角平分线交于一点，且这点在三角形内。正确的命题有( )
A.1个 B.2个 C.3个 D.4个
二 填空题
1、在△ABC中，如果∠A∶∠B∶∠C＝1∶1∶2，根据三角形按角进行分类，这个三角形__
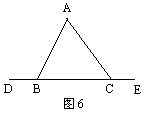
2、如图6，∠ABD与∠ACE是△ABC的两个外角，若∠A＝70°，则∠ABD＋∠ACE＝_____
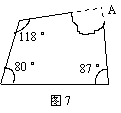
3、如图7，是一块四边形钢板缺了一个角，根据图中所标出的测量结果，得所缺损的∠A的度数为_________.
4、把命题“平行于同一条直线的两条直线互相平行”改写成“如果…，那么…”的形式为____________________________ ___________
|
5、三角形木架的形状不会改变,而四边形木架的形状会改变,这说明三角形具有______,而四边形不具有_________.
6、△ABC中,若∠B=∠A+∠C，则△ABC是 三角形.
7、三角形的两边的长分别为2cm和7cm，若第三边的长为奇数,则三角形的周长是 .
8、在△ABC中,∠A:∠B:∠C=2:3:4,则∠B=______.
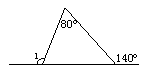
9、如图,∠1=_____.
10、在△ABC中，∠A=3∠B，∠A－∠C=30°，则∠A=____，∠B=____，∠C=______。
11、一个三角形周长为27cm，三边长比为2∶3∶4，则最长边比最短边长 。
12、一个多边形的内角和与外角和的差是180°则这个多边形的边数为_______
13小芳画一个有两边长分别为5和6的等腰三角形，则它的周长是
14、在ABC中，
的平分线相交于点P，设
用x的代数式表示
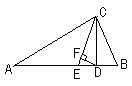
15、如图，⊿ABC中，∠A = 40°，∠B = 72°
CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF = 度。
三 解答题 (解答要求写出文字说明, 证明过程或计算步骤)
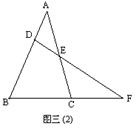1、如图三(2)，直线DE交△ABC的边AB、AC于D、E，交BC延长线于F，若∠B＝67°，∠ACB＝74°，∠AED＝48°，求∠BDF的度数
2、分别作出锐角△ABC和钝角△A1B1C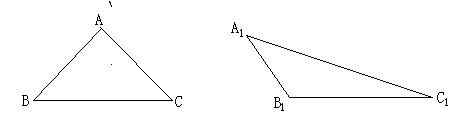
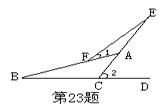
3、如图，在△ABC中，D在BC延长线上，E在CA的延长线上，F在AB上，
试说明∠2＞∠1的理由。
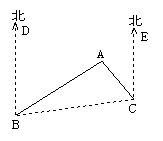
4、 如图，灯塔A在船B的北偏东50度，又在船C的西北方向，那么灯塔A看船B、船C的视角∠BAC的度数是多少？
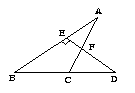
5、如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.
已知∠A=30∠FCD=80求 °
∠D
6、如图，在直角三角形ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm，求:(1)△ABC的面积； (2)CD的长；
（3）作出△ABC的边AC上的中线BE，并求出△ABE的面积；
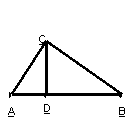（4）作出△BCD的边BC边上的高DF，当BD=11cm 时，试求出DF的长。
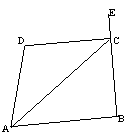7、如图，已知∠DAB+∠D=180°，AC平分∠DAB，且∠CAD=25°，∠B=95°（1）求∠DCA的度数；（2）求∠DCE的度数。
8、下面两图是分别用三根、五根火材搭成的三角形，那么用九根火材你能搭出几种不同的三角形，画出示意图，并写出三角形的类型。
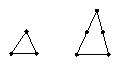
9、在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案．也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫做平面镶嵌）．这显然与正多边形的内角大小有关．当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360°）时，就拼成了一个平面图形．
⑴ （5分）请根据下列图形，填写表中空格：
⑵（2分） 如果只限于用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形？
⑶ （7分）从正三角形、正四边形、正五边形、正六边形、正八边形、正十边形、正十二边形中任选两种正多边形镶嵌，请全部写出这两种正多边形。并从其中任选一种探索这两种正多边形共能镶嵌成几种不同的平面图形？说明你的理由。