第五章 整式的乘除（5.1-5.5）
班级_______姓名_______得分_______
一、请准确填空(每空2分，共15空，合计30分)
1、一个长方体的长、宽、高分别是5a、2a、a3,则该长方体的体积为________。
2、(－x)2·(－x)5·(－x)7=________。
3、m(-m4)3=______，－2x(x2-2x-1)=___________，am=4,an=3，am+n=______。
4、(2x－1)(－3x+2)=____________。
5、(a-4)(a+4)=__________,
___________。
6、
____________________，3a2 — a（a —1）=____________。
7、若
，则
等于____________。
8、若a-b=5，ab=4，则a2+ b2的值为_________，当x = 
，y = — 
，代数式：x2—2xy + y2—2的值等于___________。
9、
是完全平方式，则k=___________。
10、如图1是一个三角尺,则图中阴影部分的面积为________。
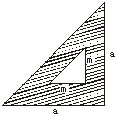
图1
二、相信你的选择(每小题2分,共20分)
11、小明做了如下四道计算题：①xm+xn=xm+n;②x3·x3=x9;③xm·x－n=xm+n;④xm÷xn=xm-n,你认为小明做对的有（ ）
A. ①③ B.①④ C.②③ D.③④
12、下列5个算式：①53+53；②2×53；③(2×52)(
×53)；④［22×()2］3；
⑤(23)2·［()2］3等于56的是（ ）
A.①②③ B.③④⑤ C.①② D.①③④⑤
13、下列计算正确的是（ ）
A.(π－3)0=0 B.4-1=－4
C.(－3)-2=－
D.(－
)-3=－
14、(－2)2004+(－2)2005的值为（ ）
A.－22004 B.22004 C.－22005 D.－2
15、下列计算错误的是（ ）
A.
B.
C.
D.
16、计算
的结果是（ ）
A.
B.
C.
D.
17、下列各式①
，②
，③
④
⑤
计算结果相同的是（ ）
A.①④ B.①⑤ C.②③ D. ②④
18、
成立的条件是（
）
A．n为奇数 B．n是正整数
C． n是偶数 D. n是负数
19、如图2，甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式：①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);④2am+2an+bm+bn，你认为其中正确的有（ ）
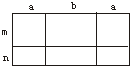
A.①② B.③④ C.①②③ D.①②③④
20、若x=2m+1,y=3+4m,用x的代数式表示y为（ ）
A.3+
B.3+x2 C.3+
D.3+4x2
三、考查你的基本功(共30分)
21、计算题(每小题分，共16分)
(1) (0.25)9·(29)2·(－
)2005·(－2
)2004
(2)
(3)
(4)利用乘法公式计算98×102－992
22、(10分)先化简，再求值.
(1) 分) 
(2) (分)已知xy2=－2,求xy(2x3y7－5x2y5－y);
23、(4分)解方程2（2y+1）2-8(y+1)(y-1)=34
四、生活中的数学(共20分)
24、（6分）为美化居民小区，需在一块空地上铺设草皮，如图中的阴影部分（单位：米）
（1）计算要铺设草皮的空地面积（用含有x的字母表示）
（2）若市场上草皮的单价为7a元/米2，则预计购买草皮至少需多少元？
 |
五、探究拓展与应用(共14分)
25、(6分)已知2a=5,2b=10,2c=50,你能找出a、b、c之间的关系吗？请说明理由.
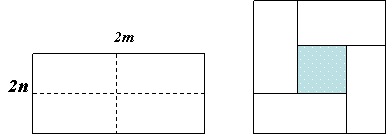
26、(8分)动手探索：25.我们把如下左图的一个长为2m，宽为2n的长方形，沿图中的虚线剪成四个小长方形，再按如下右图围成较大的正方形.
(1)大正方形的边长是多少？
(2)中间正方形（阴影部分）的边长是多少？
(3)用两种不同的方法求阴影部分的面积；
(4)比较两种方法，你能得到怎样的等量关系？
六、自我挑战（附加题：每题10分）
27、观察下列算式，你发现了什么规律？
12=
；12+22=
；12+22+32 =
；12+22 +32 + 42 =
；…
（1）你能用一个算式表示这个规律吗？
（2）根据你发现的规律，计算下面算式的值：12+22 +32 + … +82
28、观察下列算式：
44－8=62,4444－88=662,444444－888=6662,……
(1)你发现了什么规律？请用含n(n为正整数)把它表示出来;
(2)利用你发现的规律解决下列问题:
若
－
＝N2，
你能求出N的各位数字的和吗？若能求,求出它的和；若不能求,请说出理由。