立体图形竞赛练习题
一、选择题（每题5分,共30分）
1．如图1是图2中（ ）的表面展开图．
（A）甲正方体 （B）乙正方体 （C）丙正方体（D）甲正方体或丙正方体
解：从展开图可以看出，每个面上至少有一块阴影，从而排除丙；又每个面上没有相邻的阴影，从而排除乙；
故选（A）
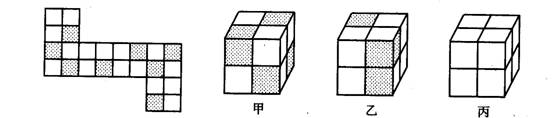
图1 图2
2．一个立方组合体的三视图如图3，则该组合体共有多少个小正方体（ ）（ ）
（A）7个或8个 （B）8个或9个 （C）9个或10个 （D）11个
解：从主视图知正面7个，从左视图、俯视图知第二排3个
故选（C）
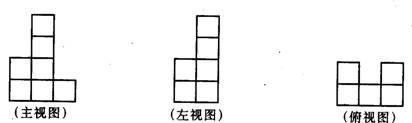
图3
3．如图4所示的立方体，如果把它剪开，可以是图（ ）
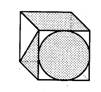图4
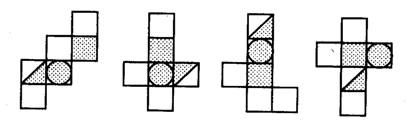
（A） （B） （C） （D）
解:选（D）
4.一个长方形折叠后能围成一个三棱柱，这个三棱柱的底面一定是（ ）
（A）三角形 （B）等边三角形 （C）等腰三角形 （D）直角三角形
解：选（A）
5．一个画家有14个棱长为
的正方体,他在地面上把它们摆成如图5所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )
(A) 
(B) 
(C) 
(D) 
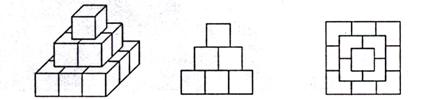
图5 图6 图7
解：:这个模型的主视图如图6,它的面积是
,其它的三个侧面的视图和它一样,故侧面积是
; 这个模型的俯视图如图7, 它的面积是
.所以涂上颜色的总面积是
.
故选(A).
二、填空题（每题5分,共30分）
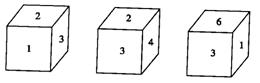
6．如图8，是标有1，2，3，4，5，6六个数字
的一个正方体的三种不同摆法。问三个正方体
朝左的一面的数字之和是______. 图8
解：有三个正方体中的已知数字可判断数字
1与4相对，2与6相对，3与5相对，
故三个正方体朝左的一面的数字和为5+1+4=10
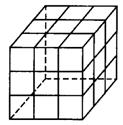
7． 如图9，是一个大正立方体，把它的每个面
都划分为9个小正方形，这个大正方体中共有多少个正方体。
解：这个大正方体中包含棱长分别为1，2，3的三类正方体，
它们的个数分别为27，8，1，所以这个大正方体所包含
的正方体的个数是27+8+1=36 图9
8． 小川用正方体木块搭建大楼，图10展示了该大楼从前面和左面看到的形状．为塔建这座大楼，需要正方体木块的最大数量是______，最小数量是______.
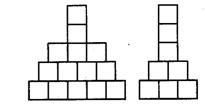图10
解：最大数量是28，最小数量是17
9． 六个立方体的可见部分如图11，图12是其中一个立方体的侧面展开图，那么它是______的侧面展开图。
图11 图12
解：填C
10．一个长方体的长、宽、高分别为
，先从这个长方体上尽可能大地切下一个正方体，再从剩余部分上尽可能大地切下一个正方体，最后再从第二次的剩余部分上尽可能大地切下一个正方体，那么，经三次切割后剩余部分的体积为
解：
三、解答题（每题10分,共40分）
11．由若干个单位立方体组成一个较大的立方体，然后把这个大立方体的某些面上涂上油漆，油漆干后，把大立方体拆开成单位立方体，发现有45个单位立方体上任何一面都没有漆．那么，大立方体被涂过油漆的面数是多少？
解:设大立方体棱长为
，显然
，又若
，即使六面都油漆过，未油漆的小方块也有
个，故
或5。又除掉已油漆过的单位立方体后，剩下未漆的构成一个长方体，设其长，宽，高为
，则
，且
，故只能是
，即
所以大立方体的四个面油漆过．
12． (1)试设计一种方法，把一个正方形不重复不遗漏地分割成8个正方形(分得的正方形大小可以不相同)；又问如何把正方形按上述要求分成31个正方形?
(2)试设计一种方法，把一个立方体分割成55个立方体(分得的立方体大小可以不相同)．
解：(1)容易把一个正方形分成
个正方形，再把其中位于一角的9个拼成一个正方形，共得
个正方形．分成16个正方形后，把其中任意5个各分成4个小正方形，共
个正方形．
(2)把立方体分割成
个立方体，再把其中4个各分成
个立方体，共
个立方体．
13．如图13，剪一块硬纸片可以做成一个多面体的纸模型(沿虚线折，沿实线粘)．这个多面体的面数、顶点数和棱数的总和是多少?
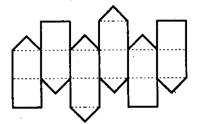图13
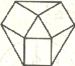图14
解：多面体的面数，可以直接从侧面展开图中数出来，12个正方形加8个三角形，共20面．图14是多面体上部的示意图，共有9个顶点；同样，下部也是9个顶点，共18个顶点．棱数要分成三层来数．上层，从示意图数，有15条，下层也是15条；中间部分为6条．一共
(条) ．
所以多面体的面数、顶点数和棱数的总和是20+18+36=74(个)．