七下第十一章“图形的全等”测试卷
一、选择题
1．下列图形中，和左图全等的图形是（ ）
 |
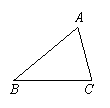
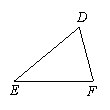2．在ΔABC和ΔDEF中，如果∠A=∠D，∠B=∠E，要使这两个三角形全等，还需要的条件可以是（
）
（A）AB=EF （B）BC=EF
（C）AB=AC （D）∠C=∠D
 |
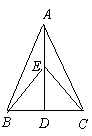3．如图，ΔABC中，AB=AC，BE=EC，直接使用“SSS”可判定（ ）
（A）ΔABD≌ΔACD （B）ΔABE≌ΔACE
（C）ΔBED≌ΔCED （D）ΔABE≌ΔEDC
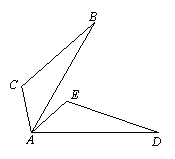
4．如图，ΔABC≌ΔADE，AB=AD，AC=AE，∠B=20º，
∠E=110º，∠EAB=30º，则∠BAD的度数为（ ）
（A）80º （B）110º （C）70º （D）130º
5．下列结论正确的是 （ ）
（A）有两个锐角相等的两个直角三角形全等；
（B）一条斜边对应相等的两个直角三角形全等；
（C）顶角和底边对应相等的两个等腰三角形全等；
（D）两个等边三角形全等.
6．
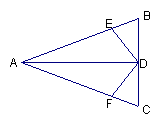已知，如图，△ABC中，AB=AC，AD是角平分线，BE=CF， 则下列说法中正确的有几个（ ）
（1）AD平分∠EDF； （2）△EBD≌△FCD；
（3）BD=CD； （4）AD⊥BC.
（A）1个 （B）2个 （C）3个 （D）4个
二、填空题
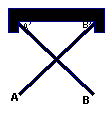
7．把两根钢条AA´、BB´的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳）， 如图， 若测得AB=5cm，则槽宽为 cm．
（第7题图） （第8题图）
8．如图，∠C=∠D，AC=BD，则根据 ，可以判断△ ≌△ ．
9．如图，在△ABC和△ABD中，∠C=∠D=90°，若利用“HL”推出△ABC≌△ABD，则可以添加条件
，或 ．
（第9题图） （第10题图）
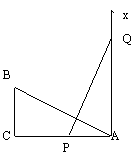
10．如图，有一个直角三角形ABC，∠C=90°，AC=10，BC=5，一条线段PQ=AB，P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动，问P点运动到 位置时，才能使ΔABC≌ΔPQA.
三、观察与思考
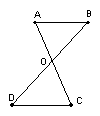
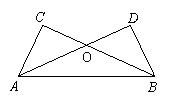
11．如图，线段AC和BD相交于O，且被点O平分，你能得到AB∥CD吗？请说明理由．
|
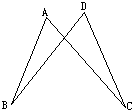
12．为了参加学校举行的风筝设计比赛，小明用四根竹棒扎成如图所示的风筝框架，已知：
AB＝CD，AC＝DB.你认为小明的风筝两脚的大小相同吗？(即∠B=∠C吗)试说明理由.
|
四、操作与解释
13．试着把下图（1）和（2）分成四个全等的图形（保留画图痕迹），并解释全等的理由。
 | |||
 | |||
（1） （2）
14．两块大小一样的含30°角的三角板,放在桌面上，可以拼出多种不同的全等图形.下面是小红拼出了的四个全等图形（如图所示）：.
请你先观察图形的特点，再结合图形的变化进行操作，画出四个有别于上图的不同图形。
五、解决问题
15．七年级（1）班同学到野外上数学活动课，为测量池塘两端A、B的距离，设计了如下方案：
（Ⅰ）如图1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，BC至E，使DC=AC，EC=BC，最后测出DE的距离即为AB的长；
（Ⅱ）如图2，先过B点作AB的垂线BF，再在BF上取C、D两点使BC=CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离.
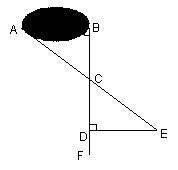
（图1） （图2）
阅读后回答下列问题：
（1）方案（Ⅰ）是否可行？请说明理由．
（2）方案（Ⅱ）是否可行？请说明理由．
（3）方案（Ⅱ）中作BF⊥AB，ED⊥BF的目的是 ；若仅满足∠ABD=∠BDE≠90°，方案（Ⅱ）是否成立？ .