第6、7、8章方程(组)、不等式(组)复习资料
&七年级一元一次方程专题辅导1
一、解一元一次方程,要求灵活运用
(1)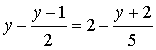 (2)
(2)![]()
(3)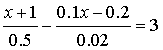 (4)
(4) 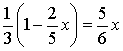
(5)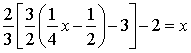 (6)
(6) ![]()
二、一元一次方程的简单应用举例:
1、当![]() 时,代数式
时,代数式![]() 的值是4,那么,当
的值是4,那么,当![]() 时,则这代数式的值为
。
时,则这代数式的值为
。
2、已知关于x的方程![]() 的根是–2,则k的值
的根是–2,则k的值
3、如果方程3x+4=0与方程3x+4k=8的解相同,则k=_________
4、当m=___时,方程![]() 是一元一次方程。
是一元一次方程。
5、如果![]() 与
与![]() 是同类项,则
是同类项,则![]() ;
;
6、若![]() ,则
,则![]() ,
,![]() 。
。
7、当x 时,代数式![]() 的值与代数式
的值与代数式![]() 的值相等。
的值相等。
8、已知![]() 是方程
是方程![]() 的解,那么关于
的解,那么关于![]() 的方程
的方程![]() 的解是多少?
的解是多少?
9、当k取何值时,代数式![]() 比
比![]() 的值小1?
的值小1?
10、当k取何值时,方程2(2x-3)=1-2x和8-k=2(x+1)的解相同?
数式的值。
三、应用题
1. 一种货物,连续两次均以10%的幅度降价后,售价为486元,则降价前的售价为__________元。
2. 某市按以下规定收取每月水费:若每月每户用水不超过20立方米,则每立方米水价按1.2元收费;若超过20立方米,则超过部分每立方米按2元收费。如果某户居民在某月所交水费的平均水价为每立方米1.5元,那么他这个月共用了_________________________立方米的水。
3. 某项工程,甲单独做要x天完成,甲、乙合做要y天完成,那么乙单独完成这项工作要的天数是_______________。
4. 甲队有32人,乙队有28人,现从乙队抽x人到甲队,使甲队是乙队人数的2倍,依题意,列出的方程是_________________。
5. 一种商品,每件成本a元,将成本增加25%定出价格,后因仓库积压减价,按价格的92%出售,每件还能盈利_____________元。
6. 工人师傅制作了一个容积是![]() ,高为6cm的长方体盒子,已知盒子底面的长比宽多5cm,那么盒子底面的宽是__________________cm。
,高为6cm的长方体盒子,已知盒子底面的长比宽多5cm,那么盒子底面的宽是__________________cm。
7. 把30克盐倒入100克水中,则盐水浓度为_______________,再加入a克水,则盐水的浓度为_________________。
8. A、B两地相距离a千米,甲每小时走5千米,乙每小时走7千米,两人分别从A、B两地同时出发,相向而行,_________________小时相遇。
9. 三个数的比是5:6:7,它们之和是198,则这三个数分别为__________________
10. 一个水池装有甲、乙、丙三个进水管,单开甲管45分钟注满水池,单开乙管60分钟注满水池,单开丙管90分钟可注满水池。如果三管一齐开_________________________分钟注满水池。
11. 为节约能源,某单位按以下规定收取每月电费:用电不超过140度,按每度0.43元收费;如果超过140度,超过部分按每度0.57元收费。若某用电户四月份的电费平均每度0.5元,问该用户四月应交电费多少元?
12. 甲、乙两队学生绿化校园,如果两队合作,6天可以完成;如果单独工作,乙队比甲队多用5天,两队单独工作各要多少天?
13. 李明以两种形式储蓄了500元,一种储蓄的年利率是5%,另一种是4%,一年后共得到利息23元5角,两种储蓄各存了多少钱?
14. 从甲地到乙地,先下山后走平路,某人骑自行车从甲地以每小时12千米的速度下山,而以每小时9千米速度通过平路,到乙地55分钟。他回来时以每小时8千米的速度通过平路,而以每小时4千米速度上山,回到甲地用![]() 小时,求甲、乙两地的距离。
小时,求甲、乙两地的距离。
15. 为了准备小勇6年后上大学的学费5000元,他的父母现在就参加了教育储蓄,下面有两种储蓄方式。 (1)直接存一个6年期,年利率是2.88%; (2)先存一个3年期的,3年后将本利和自动转存一个3年期。3年期的年利率是2.7%。 你认为哪种储蓄方式开始存人的本金比较少?
&七年级二元一次方程组专题辅导2
![]()
![]() 一、解方程组
一、解方程组
1、 2、
3、![]() 4、
4、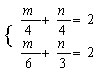
5、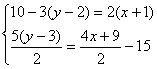
二、填空题
1、请写出一组x、y的值,使它满足方程![]() :
。
:
。
2、x的2倍与y的![]() 的和是6,可以列出方程
。
的和是6,可以列出方程
。
3、已知 ![]() 都满足方程y=kx-b,则k、b的值分别为____________________。
都满足方程y=kx-b,则k、b的值分别为____________________。
4、已知方程![]() ,写出用
,写出用![]() 表示
表示![]() 的式子得________________。当
的式子得________________。当![]() 时,
时,![]() _______ 。
_______ 。
5、已知![]() ,则x与y之间的关系式为__________________。
,则x与y之间的关系式为__________________。
6、方程![]() 的正整数解是______________。
的正整数解是______________。
7、 ![]()
8、某长方形的周长是44cm,若宽的3倍比长多6cm,则该长方形的长和宽各是_____________
9、一名学生问老师:“您今年多大?”老师风趣地说:“我像您这样大时,您才出生;您到我这么大时,我已经37岁了。” 则老师、学生今年年龄各是_________________
10、一条船顺水行驶36千米和逆水行驶24千米的时间都是3小时,则船在静水中的速度与水流的速度分别是__________________。
三、应用题
1、王大伯承包了25亩土地,今年春季改种茄子和西红柿两种大棚蔬菜,用去了44000元,其中种茄子每亩用去了1700元,获纯利2600元;种西红柿每亩用去了1800元,获纯利2600元,问王大伯一共获纯利多少元?
2、某酒店的客房有三人间和两人间两种,三人间每人每天25元,两人间每人每天 35元,一个50人的旅游团到了该酒店住宿,租了若干间客房,且每间客房恰好住满,一天共花去1510元,求两种客房各租了多少间?
3、某中学组织初一学生春游,原计划租用45座汽车若干辆,但有15人没有座位:若租用同样数量的60座汽车,则多出一辆,且其余客车恰好坐满。已知45座客车每日租金每辆220元,60座客车每日租金为每辆300元。
(1)初一年级人数是多少?原计划租用45座汽车多少辆?
(2)若租用同一种车,要使每个学生都有座位,怎样租用更合算?
4、已知一铁路桥长1000米,现有一列火车从桥上通过,测得火车从开始上桥到车身过完桥共用1分钟,整列火车完全在桥上的时间为40秒,求火车的速度及火车的长度。
5、某蔬菜公司收购到某种蔬菜140吨,准备加工后上市销售,该公司的加工能力是:每天精加工6吨或者粗加工16吨,现计划用15天完成加工任务,该公司应安排几天粗加工,几天精加工,才能按期完成任务?如果每吨蔬菜粗加工后的利润为1000元,精加工后为2000元,那么该公司出售这些加工后的蔬菜共可获利多少元?
6、李明以两种形式分别储蓄了2000元各1000元,一年后全部取出,扣除利息所得税可得利息43.92,已知两种储蓄年利率的和为3.24%,问这两种储蓄的年利率各是百分之几?(注:公民应交利息所得税=利息金额×20%)。
7、甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50﹪的利润定价,乙服装按40﹪的利润定价。在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?
8、某同学在A、B两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元。
(1)求该同学看中的随身听和书包单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
9、一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这种货车的情况如下表:
| 项目 | 第一次 | 第二次 |
| 甲种货车辆数/辆 | 2 | 5 |
| 乙种货车辆数/辆 | 3 | 6 |
| 累计运货吨数/吨 | 15.5 | 35 |
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问:货车应付运费多少元?
10、某玩具工厂广告称:“本厂工人工作时间:每天工作8小时,每月工作25天;待遇:熟练工人按计件付工资,多劳多得,计件工资不少于800元,每月另加福利工资100元,按月结算;……”该厂只生产两种玩具:小狗和小汽车。熟练工人晓云元月份领工资900多元,她记录了如下表的一些数据:
| 小狗件数(单位:个) | 小汽车个数(单位:个) | 总时间(单位:分) | 总工资(单位:元) |
| 1 | 1 | 35 | 2.15 |
| 2 | 2 | 70 | 4.30 |
| 3 | 2 | 85 | 5.05 |
元月份作小狗和小汽车的数目没有限制,从二月分开始,厂方从销售方面考虑逐月调整为:k月份每个工人每月生产的小狗的个数不少于生产的小汽车的个数的k倍(k=2,3,4,……,12),假设晓云的工作效率不变,且服从工厂的安排,请运用所学数学知识说明厂家广告是否有欺诈行为?
&七年级一元一次不等式(组)专题辅导3
一、填空题
![]()
![]() 1、不等式组 x<2 的解集是 x<-4 的解集是
1、不等式组 x<2 的解集是 x<-4 的解集是
x>-4 x>2
![]()
![]() -x>3
2-3x≤8
-x>3
2-3x≤8
不等式组 的解集是 的解集是
x<-2
![]() x-1<1
x-1<1
2、若a<b,用“<”或“>”号填空:
(1)a+l b+l; (2)a-5 b-5; (3)-3a -3b; (4)6-a 6-b.
3、写出适合不等式2x+3<9的正整数解_____________________。
![]() 1-x≥0
1-x≥0
4、不等式组 的整数解是 .
2x-1>-3
5、代数式1-k的值大于-1而又不大于3 ,则k的取值范围是 。
二、解答题
1、解不等式和不等式组,并把解集表示在数轴上:
(1) ![]() (x-1)≥1;
(2)3y-
(x-1)≥1;
(2)3y-![]() >
>![]() y+1
y+1
![]()
![]() (3) 2x+3>5
(4) 11-2(x-3)≥3(x-1)
(3) 2x+3>5
(4) 11-2(x-3)≥3(x-1)
3x-2≤4
x-2>![]()
2、当x取什么值时,代数式![]() -1的值不小于
-1的值不小于![]() +2的值?
+2的值?
三、应用题
1、现有住宿生若干,分住若干间宿舍,若每间住4人,还有19人无宿舍住;若每间住6人,则有一间宿舍不空也不满,求住宿人数和宿舍间数。
2、某校八年级(1)班计划全班同学分成若干组开展数学探究性活动.如果每个组3人,则还余10人;如果每个组5人,则有一个组的学生数最多只有1人.求该班在数学探究性活动中计划分的组数和该班学生数。
3、把一堆苹果分给几个孩子,如果每人分3个,那么多8个;如果前面每人分5个,那么最后一人得到的苹果不足3个,问有几个孩子?有多少只苹果?
4、商场出售的A型冰箱每台售价为2190元,每日耗电量为1度,而B型节能冰箱每台售价虽比A型冰箱高出10%,但每日耗电量却为0.55度.现将A型冰箱打折出售(打一折后的售价为原价的1/10),问商场至少打几折,消费者购买才合算(按使用期为10年,每年365天,每度电0.40元计算)?
5、某校校长暑假将带领该校“市级三好学生”去三峡旅游,甲旅行社说:如果校长买全票一张,则其余学生可享受半价优惠;乙旅行社说:包括校长在内全部按全票的6折优惠。已知两家旅行社的全票价都是240元,请你就学生数说明哪家旅行社更优惠?
6、某商场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如果月初出售可获利15%并且可用本和利再投资其他商品,到月末可获利10%;如果月末出售,可获利30%但要出仓储费用700元,请问根据商场的资金状况,如何购销获利较多?
7、某自行车厂今年生产销售一种新型自行车,现向你提供以下有关信息:
(1)、该厂去年已备有这种自行车车轮10000只,车轮车间今年平均每月可生产车轮1500只,每辆自行车需装配2只车轮。
(2)该厂装备车间(自行车最后一道工序生产车间)每月至少可装配这种自行车1000辆,但不超过1200辆。
(3)该厂已收到各地客户今年订购这种自行车14500辆的订货单。
(4)这种自行车出厂销售单价为500元/辆,设该厂今年这种自行车销售金额为a万元。
请你根据上述信息,判断a的取值范围。