重庆一中初2008级下期数学半期试题 2006.4
一.选择题.(每小题3分,
)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1.下列关于单项式
的次数和系数的说法正确的是( )
A.次数为5,系数为-3 B.次数为3,系数为-3
C.次数为3,系数为-9 D.次数为5,系数为-9
2.下列运算正确的是( )
A.
B.
C.
D.
3.下列各组线段中,能组成三角形的一组是( )
A.2, 1, 4 B.3, 8, 4 C.5, 7, 12 D.4, 3, 6
4.下列说法正确的是( )
A.近似数4.60与4.6的精确度相同
B.近似数5千万与近似数5000万的精确度相同
C.近似数4.31万精确到0.01
D.1.45
104精确到百位
5.已知△ABC≌△ADE,BC的延长线交DE于F,
∠B=∠D=25°,∠ACB=∠AED=105°,∠DAC=10°,
|
A.60° B.45°
C.30° D.95°
6.小明抛两枚相同质地均匀的硬币,他先抛第一枚,再抛第二枚,则两次抛得结果一样的概率是( )
A.
B.
C.
D.无法确定
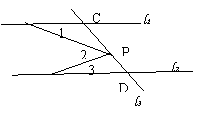7.如图,直线
,直线
和
交于C、D
两点,P为CD上一点,则∠1, ∠2, ∠3的关系是( )
A.∠2>∠1+∠3 B.无法确定
|
8.初一年级的学生准备去快乐岛旅游,从学校出发经过石湖就可到达目的地,学校到石湖有两条路,石湖到快乐岛有三条路,每条公路的长度如下图所示,同学们任选一条从学校到快乐岛的路线,则这条路线正好是最短路线的概率是( )
 | |||
 | |||
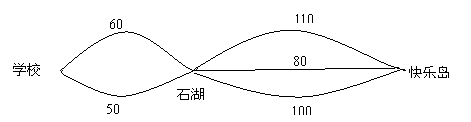A.
B.
C.
D.无法判断
9.若:
,则
的值是( )
A.4
B.
C.
D.
10.下列条件中,不能判断△ABC≌△DEF的是( )
A.∠A=∠D, ∠C=∠F, AC=DF
B.∠A=∠D, AB=DE, BC=EF
C.AC=DF, AB=DE, ∠A=∠D
D.AB=DE, ∠A=∠D=80°, ∠B=60°, ∠F=40°
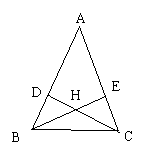
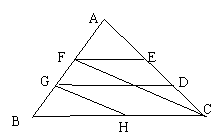
11.如图所示,H是△ABC的高CD,BE的交点,
且AD=AE,则下列结论成立的有( )
①DH=HE ②BE=CD
|
A.1个
B.2个
C.3个 D.4个
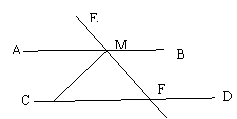
12.如图:EF//DG//BC,CF//GH,图中与∠1相等
的角有( )
A.3个 B.5个
C.6个 D.7个
|
二.填空题.(每小题4分,
)
| 题号 | 13 | 14 | 15 | 16 | 17 | 18 |
| 答案 | ||||||
| 题号 | 19 | 20 | 21 | 22 | 23 | 24 |
| 答案 |
13.多项式
是关于
的一次多项式,则= ,
= .
14.已知∠A=74°32′,则与∠A互补的角的度数为
.
15.已知
,则
=
.
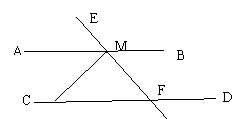
16.如图:已知AB//CD,MN⊥EF于M, ∠BME=110°,
则∠MND= , ∠MFN= .
|
6瓶啤酒.其中特种可乐和普通可乐是含有咖啡因的饮料,
那么从冰柜里随机取一瓶饮料,该饮料含有咖啡因的概率
是
. 
18.计算:
=
.
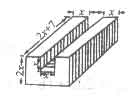19.用含有的代数式表示如图槽形钢木的
体积 .
20. (1)已知
,则
=
.
(2)已知:
,则
=
.
21.科学家发现一种病毒长度为0.67954微米,则精确到千分位的长度是 微米,结果有 个有效数字.
22.纳米技术是一项很先进的技术,它的应用很广泛,1纳米为10亿分之一米,即
米,人体内一种细胞的形状可以近似地看成圆,它的直径为1470纳米,则它的直径为
米(保留两个有效数字).
23.在△ABC中,∠A=50°,CD,BE分别是AB,AC边上的高,且CD,BE交于点P,则∠BPC的度数为 .
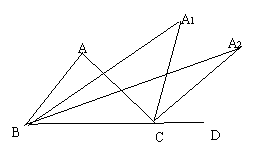24.如图,在△ABC中,延长BC到D.∠ABC与∠ACD
的平分线相交于点A1, ∠A1BC与∠A1CD的平分线
相交于点A2,依次类推, ∠A3BC和∠A3CD的平分线
相交于点A4.已知: ∠A4=6°,则∠A= .
三.计算.(25,26,27题各6分,
)
25. 
26. 
27. 
四.解答题.(28题6分,29题8分,30题8分)
28.某地区有关部门为了了解中小学生的视力情况,从该地区小学、初中、高中三个学段中各随机抽取300名学生做视力调查.根据调查获得的数据,绘制成下图所示的统计图,请根据统计图提供的信息回答下列问题.
(1)在被调查的300名初中学生中,视力不良的男生有 人,视力不良的女生有 人,视力不良的学生占本学段被调查人数的 %,以此估计该地区12000名初中生中,视力不良的人数为 人.
(2)根据调查结果,估计这个地区中小学生视力不良率随着年级的升高而 ,高中视力不良率约是小学生的 倍(结果精确到0.1倍)
中小学生视力不良人数统计图
29.填空.
如图:连接BC
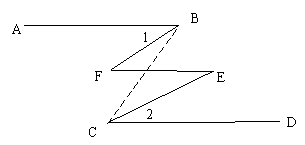∵AB//CD(已知)
∴ = ( )
又∠1=∠2(已知)
∴∠FBC=∠BCE( )
∴ // ( )
∴∠E=∠F( )
30.化简求值:
其中: 
五.证明题.(31题7分,32题7分,33题12分)
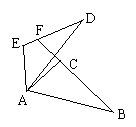
31.已知:AB//DE,AB=DE,AF=DC,请问图中有几对
全等的三角形,试一一写出,并任选其中一对加
以证明.
32.在△ABC中,∠A+∠B=2∠C, ∠A-∠C=40°.
(1)试判断△ABC的形状,并说明理由;
(2)已知△ABC中,两边分别为2cm, 5cm.且三角形的周长为一偶数,求△ABC的第三边长度及△ABC的周长.
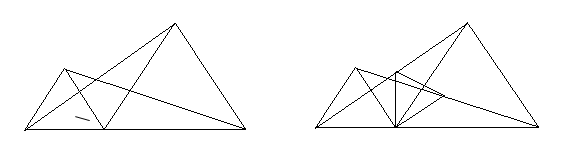
33.阅读下面材料.如图(1)把△ABC沿直线BC平行移动线段BC的长度, 可以变到
△ECD的位置.如图(2)以BC为轴把△ABC翻折180°,可以变到△DBC的位置.如图(3)以A为中心把△ABC旋转180°可以变到△AED的位置,像这样,其中一个三角形是由另一个三角形按平行移动,翻折,旋转等方法变成的,这种只改变位置不改变形状大小的图形变换叫做三角形的全等变换.
 | |||||
 | |||||
 | |||||
 |
(1) (2) (3)
如图(4)线段BE上有一点C,以BC,CE为边,分别在BE的同侧作等边△ABC,△DCE
,连接AE,BD,分别交CD,CA于Q,P.
(1)找出图(4)中有几组全等三角形,请一一写出,并分析每组中的两个三角形是分别经过怎样的图形变化相互重合的? 试试找出图中有哪几组相等的线段(等边三角形中各边除外)
(2)如图(5)取AE的中点M,BD的中点N,连接CN,CM,MN,试判定△CMN的形状,并说明理由.
(4) (5)
命题人:白 薇 游兴政
重庆一中初2008级下期数学半期试题答案 2006.4
一.选择题.(每小题3分,)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | D | D | A | A | D | B | D | B | D | B |
二.填空题.(每小题4分,)
13.
14.105°28′
15.
16.20°, 70°
17.
18.
19.
20.
21.0.680, 3 22.
23.50°或130° 24.96°
三.计算.(25,26,27题各6分,)
25.
解:原式
26.
解:原式
27.
解:原式
四.解答题.(28题6分,29题8分,30题8分)
28.(1)65, 79, 48, 5760
(2)升高, 3.6
29.(每空1分)
∠ABC=∠BCD 两直线平行内错角相等
等式的性质
BF//CE 内错角相等两直线平行
两直线平行内错角相等
30.化简求值
解:原式:
(*)
又∵
∴
∴
代入(*)式 得
五.证明题.(31题7分,32题7分,33题12分)
31.有三对全等三角形:分别是:△AFB≌△DCE
△ACB≌△DFE
△FBC≌△CEF
∵AB//DE(已知) ∴∠A=∠D (两直线平行内错角相等)
∴在△AFB和△DCE中
又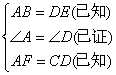
∴△AFB≌△DCE（SAS）
32.∵在△ABC中,∠A+∠B+∠C=180° 又∠A+∠B=2∠C
(1)∴3∠C=180° ∴∠C=60°
又∠A-∠C=40° ∴∠A=100°
∴△ABC为钝角三角形
(2)设△ABC第三边长为
,则由三角形三边不等关系得:
∴
∵△ABC的周长为一偶数
∴周长为:
∴△ABC第三边为5cm,且周长为12cm.
33.(1)①△BCD≌△ACE:将△BCD绕点C顺时针旋转60° 即可得到△ACE (2分)
②△PCD≌△QCE:将△PCD绕C点顺时针旋转60°即可得到△QCE(2分)
③△BCP≌△ACQ:将△BCP绕点C顺时针旋转60°,即可得到△ACQ(2分)
相等的线段有BD=AE, CP=CQ, BP=AQ, DP=QE(1分)
(2)∵△BCD≌△ACE ∴∠NDC=∠MEC, BE=AE （5分）
又∵M、N分别为AE、BD的中点
∴ND=AE=BD=AE
又∵DC=CE ∴△NDC≌△MEC(AAS)
∴CN=CM
又∠NCD=∠MCE
∴∠NCD+∠DCM=∠MCE+∠DCM
∴∠NCM=∠DCE=60°
又∵CN=CM
∴△CMN是等边三角形