2006—2007初七年级下半期数学测试题
时间：120分钟 总分：150分
 |
一、精心的选一选(（本大题共12小题，每小题4分，满分48分；在每小题给出的四个选项中，选出正确的一个)
1．计算
的结果是（
）
A．a5 B．a6 C．a8 D．a9
2．下列计算中，正确的是（ ）
A．(a + b)2 = a2 + b2 B．a3 + a2 = 2a5
C．(－2x3)2=4x6 D．(－1)—1=1
3．x – (2x – y)的运算结果是（ ）
A．－x + y B．－x－y C．x－y D．3x－y
4．已知同一平面内的直线L1，L2，L3，如果L1⊥L2，L2⊥L3，那么L1与L3的位置关系是（ ）
A．平行 B．相交 C．垂直 D．以上全不对
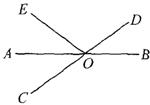5．如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC=70°，则∠BOD的度数等于（ ）
A．30° B．35°
C．20° D．40°
6．2003年10月15日，中国“神舟”五号载人飞船成功发射，圆了中国人千年的飞天梦，航天员杨利伟乘飞船在约21小时内环绕地球14圈，其长度约为千米，用科学记数法表示为（ ）
A．5.91×107千米 B．5.91×108千米
C．5.91×109千米 D．5.91×1010千米
7.天安门广场的面积约为44万平方米，请你估计一下，它的百万分之一约相当于（ ）
A．教室地面的面积 B.黑板面的面积
C.课桌的面积 D.铅笔盒盒面的面积
8．下列运算正确的是（ ）
A．3a + 2b = 5ab B．(a – 1)2=a2 – 2a + 1
C．a6 ÷ a3 = a2 D．(a3)2 =a5
9．一学员在广场上练习驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是（ ）
A．第一次向左拐30°，第二次向右拐30°
B．第一次向右拐50°，第二次向左拐130°
C．第一次向右拐50°，第二次向右拐130°
D．第一次向左拐50°，第二次向左拐130°
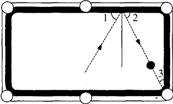
10．如图，∠1=∠2，若∠3=30°，为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时必须保证∠1为( )
A．30° B．45°
C．60° D．75°
11、计算
得（
）
A．1 B．－1 C．
D．－
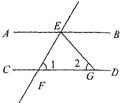
12．如图，已知AB∥CD，直线EF分别交AB，CD于点E，F，EG平分∠BEF，若∠1=50°，则∠2的度数为（ ）
A．50° B．60°
C．65° D．70°
二、细心的填一填(本大题共12小题，每小题3分，满分36分)
13．2a2·a3÷a4=_________。
14．若(a – 1)2与b + 1的值互为相反数，则a + b =_________。
15．若
与
的和为一个单项式，则x=_________。
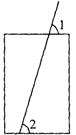
16．如图，用一根吸管吸吮易拉罐内的饮料时，吸管与易拉罐上部夹角∠1=74°，那么吸管与易拉罐下部夹角∠2=_________。
17．2003年10月15日9时，航天英雄杨利伟乘“神舟”五号载人飞船首次发射升空，于9时9分50秒准确进入预定轨道开始飞行，飞了十四圈，飞行路程约为6.01×105千米，这个路程保留有哪几个有效数字_________。
18．2003年6月1日9时，举世瞩目的三峡工程正式下闸蓄水，首批4台机组率先发电，预计年内可发电度，这个数用科学记数法表示，记为_________度；近似数0.30精确到_________位，有_________个有效数字。
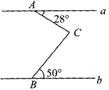19．如图，直线a∥b，则∠ACB=_________。
| |
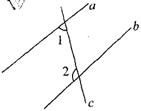20．如图，两条直线a，b被第三条直线c所截，如果a∥b，∠1=70°，那么∠2=_________。
21．多项式4x2+1加上一个单项式后，使它能成为一个整式的完全平方，则加上的单项式可以是_______（填上一个你认为正确的即可，不必考虑所有的可能情况。
22、化简：
=
23.化简：(a – 1)2= ； ．a6 ÷ a3 = 。
24.瑞士中学教师巴尔末成功地从光谱数据
中得到巴尔末公式，从而打开了光谱奥妙的大门。请你按这种规律写出第七个数据是＿＿＿＿＿。
 |
三、认真的解一解：(共10题，共66分)
25．计算下列两个小题：
(1)(a + 2b)(3a – 7b);(6分) (2)(16x2y3z+8x3y2z)÷8x2y2 (6分)
26．已知
，求A+B；(6分)
27．先化简下面的代数式，再求值：(8分)
，其中
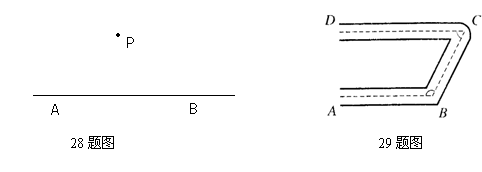28．（用尺规作图，不写作法，保留作图痕迹）重庆市某地有一段笔直的公路AB，因交通阻塞严重，为缓解这段公路交通压力，准备过P点修一条与AB平行的公路，请你来当一回设计师。 (4分)
29．如图，一个合格的弯形管道ABCD需要AB边与CD边平行，现测得某个管道的拐角∠ABC=120°，∠BCD=60°，这个管道符合要求吗？为什么?（4分）
30．如图所示，(横线填结论，括号内批上理由，4分)
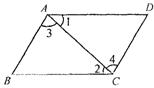（1）∵AB//CD(已知)
∴ = ( )
（2）∵AD//BC(已知)
∴ = ( )
31．如图，已知AB∥DE, AE∥DC 求证∠1=∠2 (6分)
 |
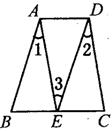32．如图，已知CD⊥AB，EG⊥AB，∠1=∠2，AC⊥DE，则BC和AC的位置关系是什么？(7分)
 |
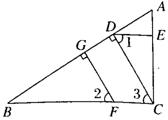33．解方程：(x + 
)(x － ) – 2x(x + 
) = 0(6分)
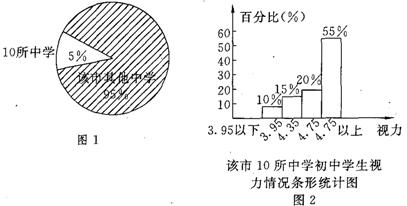
34．初中学生的视力状况已受到全社会广泛关注，某市有关部门对全市20万名初中学生视力状况进行了一次抽样调查，从中随机抽查了10所中学全体初中学生的视力，图1，图2，是2005年抽样情况统计图，请根据下图解答以下问题：①2005年这10所中学初中学生的总人数有多少人？
②2005年这10所中学的初中学生中，视力在4.75以上的学生人数占全市初中学生总人数的百分比是多少？
③2005年该市参加中考的学生达66000人，请你估计2004年该市这10所中学参加中考的学生共有多少人？(9分)
参考答案：
一、精心选择：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | A | A | B | B | C | B | A | C | A | C |
二、13.2a； 14.0； 15.1； 16.74。； 17.6、0、1； 18.5.5×109 、百分、2；
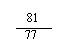19.78．；
20.110。
21.4x或-4x； 22.6a2b-1 ； 23.a2-2a+1； 24.
三、25（1）3a2-ab-14b2；（2）2yz+xz； 26.8； 27.x2+2x-2 、-2；28.略；
29.符合要求，根据同旁内角互补，两直线平行。
30.（1）∠3、∠4、两直线平行，内错角相等。（2）∠1、∠2、两直线平行，内错角相等
31.证明：∵AB∥DE
∴∠1=∠3
∵AE∥DC
∴∠3=∠2
∴∠1=∠2
32.略。
33.x=
34.(1)10000人；（2）2.75%；（3）3300人。