2003年第十四届“希望杯”全国数学邀请赛(初一笫2试)
一、选择题:(每小题5分,共50分)
1.某班有30名男生和20名女生,60%的男生和30%的女生参加了天文小组,该班参加天文小组的人数占全班人数的( )
(A)60%; (B)48%; (C)45%; (D)30%
2.
=( )
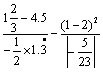(A)-
; (B)-
; (C)-
; (D)-
.
3.数轴上的点A、B、C分别对应数0、-1、x,C与A的距离大于C与B的距离,则( )
(A)x>0; (B)x>-1; (C)x<-
; (D)x<-1
4.对任意的三个整数,则( )
（A）它们的和是偶数的可能性小; (B)它们的和是奇数的可能性小;
(C)其中必有两个数的和是奇数; (D)其中必有两个数的和是偶数;
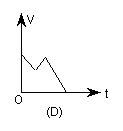
5.油箱装满油的一辆汽车在匀速行驶,当汽油恰剩油箱体积的一半时就加满油,接着又按原速度行驶,到目的地时油箱中还剩有
体积的汽油.设油箱中所剩汽油量为V(升),时间为t(分钟),则v与t的图象是( )
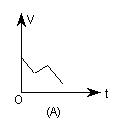
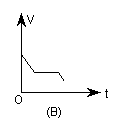
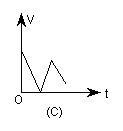
6.将长为12的线段截成长度为整数的三段,使它们成为一个三角形的三边,则构成的三角形( )
（A）不可能是等腰三角形; (B)不可能是直角三角形;
(C)不可能是等边三角形; (D)不可能是钝角三角形.
7.有一个最多能称16kg的弹簧称,称重时发现,弹簧的长度(cm)与物体的重量(kg)之间有一定的关系.根据下荚考虑:在弹簧称重范围内,弹簧最长为( )cm
| 重量(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| 长度(cm) | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 | 8.0 |
(A)18; (B)19; (C)20; (D)21
8.If<a>=
for aii integers(整数)a,an b=<8>,then<b>is( )
(A)36;(B)72;(C)666;(D)1332
9.有一串数:-2003,-1999,-1995,-1991,┉,按一定的规律排列,那么这串数中前( )个数的和最小.
(A)500; (B)501; (C)502; (D)503
10.“希望杯”四校足球邀请赛规定:
(1)比赛架采用单循环赛形式;
(2)有胜负时,胜队得3分,负队得0分;
(3)踢平时每队各得1分.
北赛结束后,四个队各自的总得分中不能出现( )
(A)8分; (B)7分; (C)6分; (D)5分;
二、填空题:(每小题5分,共50分)
11.如果方程2003x+4a=2004a-3x的根是x=1,则a=______.
12.图1中的大,小正方形的边长均为整数(cm),它们面积之和等于74cm2,则阴影三角形的面积等于________cm2.
13.如果x2+x-1=0,则x3+2x2+3=_________.
14.If a,b,c,d are rational numders(有理数),丨a-b丨≤9,丨c-d丨≤16 and 丨a-b-c+d丨=25,then丨b-a丨-丨d-c丨=___________.
15.a和
都是正整数,则a=___________.
16.如图2,ABCD是平行四边形,E在AB上,F在AD上,SΔBCE=2SΔCDF=
S
ABCD=1,则SΔCEF=____.
17.用中心角为1200,半径为6cm的扇形卷成一个圆锥(没有重叠),这个圆锥的表面积是______cm2.
18.画一条直线,可将平面分成2个部分,画2条直线,最多可将平面分成4个部分,那么,画6条直线,最多可将平面分成_______个部分.
19.a与b互为相反数,且丨a-b丨=
,那么
=_____________.
20.正整数m和n有大于1的公灼数,且满足m3+n=371,mn=___________.
三、解答题:(要求写出推算过程.21,23题各15分,22题20分)
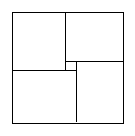
21.某同学想用5个边长不等的正方形,拼成如图3所示的大正方形.请问该同学的想法能实现吗?如果能实现,试求这5个正方形的边长;如果不能,请说明理由.
22.规定:正整数n的“H运算”是:
①当n为奇数时,H=3n+13;
②当n为偶数时,H=n×
×┉(其中H为奇数).
如:数3经过1次“H运算”的结果是22,经过2次“H运算”的结果是11,经过3次“H运算”的结果是46.
请解答:
(1)数257经过257次“H运算”的结果.
(2)若“H运算”②的结果总是常数a,求a的值.
23.救灾指挥部,将救灾物资装入34个集装箱:4吨的集装箱3个,3吨的集装箱4个,2.5吨的集装箱5个,1.5吨的集装箱10个,1吨的集装箱12个,那么至少需要多少辆载重量5吨的汽车才能一次将这些救灾物品运走?提出你的运输方案.
参考答案:
一.BACDA,DDCBA.
二.
11.1.003;
12.7;
13.4;
14.-7;
15.4;
16.
;
17.16
;
18.22;
19.
;
20.196.
三.
21.答:不能实现.
理由:假设能够实现,不妨设中间小正方形的边长为x(x>0),左下角的正方形的边长为y(y>0),则左上角的正方形的边长为(y-x),右上角的正方形的边长为(y-2x),于是有右下角的正方形的边长为(y-3x)或(y+x).
所以,y-3x=y+x,
于是4x=0,得x=0.
与x>0矛盾,所以该同学的想法不能实现.
22.(1)一个正整数n经达一次“H运算”的结果是b,记为:n
b,则257经过
笫1次“H运算”:257 257×3+13=784;
笫2次“H运算”:784 784×
=49;
笫3次“H运算”:4949×3+13=160;
笫4次“H运算”:160 160×
=5;
笫5次“H运算”:55×3+13=28;
笫6次“H运算”:28 28×
=7;
笫7次“H运算”:77×3+13=34;
笫8次“H运算”:34 34×=17;
笫9次“H运算”:1717×3+13=64;
笫10次“H运算”:64 64×
=1;
笫11次“H运算”:11×3+13=16;
笫12次“H运算”:16 16×=1;
笫13次“H运算”:11×3+13=16;
笫14次“H运算”:16 16×=1;
从笫11步以后出现循环,奇数步的结果为16,偶数步的结果为1.
因此,笫257步后的结果为16.
(2)若对一个正整数进行若干次“H操作”后出现循环,此时“H运算”②的运算结果总是a,则a一定是个奇数,那么,对a进行“H运算”①的结果a×3+13是偶数.
再对a×3+13进行“H运算”,即
a×3+13乘以
的结果仍是a,
于是
=a,
也即a×3+13=a×2k,
即a×(2k-3)=13=1×13.
因为a是正整数,
所以2k-3=1或2k-3=13,
解得k=2或k=4.
当k=2时,a=13;
当k=4时,a=1.
23.为了用载重量5吨的汽车将救灾物品一次运走,我们应将不同规格的集装箱进行有效组合,即尽量使每一节汽车都能装满.
由题设可知,物资总重63.5吨,而12<63.5÷5<13,由此可知,要把救灾物品一次运走,需要的汽车不能少于13辆.
于是我们提出如下设计方案:
A类:每辆装4吨集装箱1个和1吨集装箱1个,按排3辆汽车;
B类:每辆装3吨集装箱1个和1吨集装箱2个,按排4辆汽车;
C类:每辆装2.5吨集装箱2个,按排2辆汽车;
D类:每辆装2.5吨、1.5吨、1吨集装箱各1个,按排1辆汽车;
E类:每辆装1.5吨集装箱3个,按排3辆汽车;
而3+4+2+1+3=13(辆),
因此,要把救灾物品一次运走,需要汽车至少13辆.