初一年级数学复习试卷
一．填空： (3′×11)
1． 已知二元一次方程3x-2y=1，用含x的代数式表示y的形式是_____________;当y＞1时,x的取值范围是_____________.
2． 方程2x+y=7的正整数解共有_________组;
3．已知2x
+5y
=5是关于x，y的二元一次方程，则m
=__________.
4．某商品在进价每件a元的基础上加价50%标价,再打八折出售,则可获利__________%.
5．已知△ABC的三边分别是2，2x-1，3，则整数x=___________.
6． △ABC中，AB=AC，∠A+∠B=130°,则 ∠A=__________°.
7. 若一个多边形的内角和等于1260°, 则它一共有___________条对角线.
8．等腰三角形中，一腰上的中线把这个三角形的周长分成9㎝和6㎝两部分,则这个三角形的腰长=__________㎝,底边长=______________㎝.
9. 在正方体骰子的六个面上分别标上一个数字,使得1朝上的成功率为
,请你设计一个
标写数字的方案__________________________.
10.用都含有30°角且大小完全一样的两块三角板,取相等的边不重叠地拼合在一起,如右图所示: 除此之外,还可拼出成轴对称图形的有____________________. 不成轴对称图形的有_________________.(请画出草图).
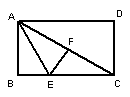11.已知长方形ABCD,先沿对角线AC对折,再沿AE对折,使AB落在
AC 上,B点与F点重合,且点A与点C关于EF对称,若AB=1,
则AC=__________, ∠ACB=____________°.
二.选择题:( 3′×9 )
19. 若不等式ax-a＞1-x的解集是x＜1,则a必须满足的条件是（ ）
（A）a＞1 (B)a＜1 (C)a＞-1 (D) a＜-1
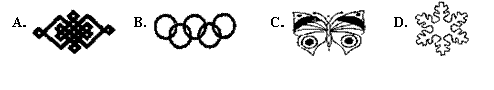20．下列轴对称图形中（如图），只有两条对称轴的图形是( )
21.下列正多边形的组合中,能够铺满地面的是( )
(A) 正八边形和正方形 (B) 正五边形和正方形
(C) 正六边形和正方形 (D) 正三角形和正八边形
22. 一个正方形截去一个角以后,所得到的多边形的内角和S的范围是:
180°＜S＜540°,则正确的截角方式是( ) (图中阴影部分表示被截去的部分)
(A)
（B）
（C）
（D）
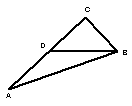
23．已知：直角三角形ABC中，∠C=90°，D是AC上一点，CD=CB，
AD=BD。则∠A等于（ ）
（A）30° （B）28﹒5° （C）22﹒5° （D）15
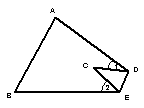
24.三角形纸片ABC中,∠A=75°, ∠B=65°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=25°,则∠2等于( )
(A)75° (B)65° (C)55° (D)45°
25．△ABC的三边长均为整数，周长为14，且其中一边为4，则 这
个三角形的最大边是（ ）
（A）5 （B）6 （C）7 （D）8
26. 若a，b，c是△ABC的三边，则式子（a+b+c）（a-b-c）（a-b+c）（a+b-c）一定（ ）
（A）大于0 （B）等于0 （C）小于0 （D）不大于0
27．下列事件中是确定事件的是（ ）．
（A）在2008年奥运会上，刘翔将再获110米栏冠军 （B）地球绕太阳公转
（C）“五一”黄金周期间，登泰山一定能观到日出 （D）打开电视机，正在播放新闻
三．解答题:(4′×2)
29.解方程组：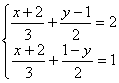
30. 解不等式组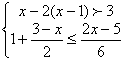
31.尺规作图（保留作图痕迹）： 图示直线L表示大运河，大运河L的同侧有A、B两村庄.
要在河边建一码头，需修建村级公路.
（1）如果建造公路，资金要两村平均摊牌（即码头到A、B两村距离相等），求码头P的位置.
（2）如果建造公路要两村集资合造，要使费用最低（即码头到A、B两村的距离之和最短），求码头P的位置.
（3）“发展农村经济，公路修到村口”。现在除了有大运河L，还有了两条公路m、n，形成了交通网.A、B两村准备合资办一家企业,问如何选址，方能使新办企业到直线m、n、L的距离相等？请你帮他们找出满足条件的点. (6分)
（1） （2） （3）
32. 已知：如图，AB=AD，∠1=∠2=∠3，BE=10
试求线段DC的长，并说明理由.(
5分)
33.应用题: 学校组织初一同学春游,原计划租用45座客车若干辆,但有15人没有座位;如果租用同样数量的60座大客车,则多出一辆,且其余客车恰好坐满.已知45座客车日租金为每辆220元,60座大客车客车日租金为每辆300元.
（1）初一年级学生有多少人? 原计划租用45座客车多少辆?
（2）要使每个学生都有座位,怎样租用更合算?最低租金是多少? (5分)
34.已知方程组
的解x,y满足x＞0,y＞0.
(1)求a的范围 (2)化简4a+5-2a-4 (6分)
35.已知:如图所示, 等边△ABC中, BO,CO分别平分∠ABC和∠ACB, EF, GH分别垂直
平分BO,CO, EF,GH交BC于点F, H.
(1)求证: OF∥AB
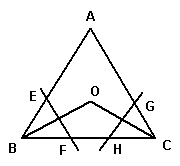(2) 若等边△ABC的边长为6㎝, 求FH的长. (6分)