七年级下学期期末数学试题

七年级下学期期末数学试题

姓名　　　　　 　　　　　　　分数　　　　 

亲爱的同学们：

祝贺你完成了七年级的学习，现在是展示你学习成果之时，希望你能尽情地发挥，祝你成功！

一、看谁的命中率高（本题有10个小题，每小题2分，共20分）

1．在下列图案中，不能用平移得到的图案是（　　 ）

　　　　  　　　　 　　　　　　

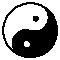
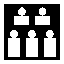
A．　　　　　　  B．　　　　　　 C．　　　　　　　　 D．

2．下面四个图形中，∠1与∠2是对顶角的是（　　）

　　　　　 　　　 　　　　

A．　　　　　　　  B．　　　　　　  C．　　　　　　　 D．

3．已知y轴上的点P到原点的距离为5，则点P的坐标为（　　　）

A．（5，0）　　　　　　　　　　　 B．（0，5）或（0，5）

C．（0，5）　　　　　　　　　　　 D．（5，0）或（5，0）

4．下列各图形中，具有稳定性的是（　　　 ）

　　　　　　　　 

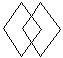
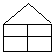
A．　　　 B．　　　C．　　　 D．　　　　　　　　  第6题图

5．一幅美丽的图案，在某个顶点处由四个边长相等的正多边形镶嵌而成，其中三个分别为正三角形、正四边形、正六边形，则另一个为（　　 ）

A．正三角形　　　 B．正四边形

C．正五边形　　　 D．正六边形

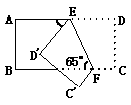
6．如图，把长方形纸片沿EF折叠， D、C分别落在、的位置，若∠EFB = 65°，则∠AE等于（　　　）

A．50°　 B．55°　 C．60°　 D．65°

7．若 2X+3=6，则X的值是（　　 ）

A．1　　　　　  B．1.5　　　　C． 2　　　　 D．2.5

8．不等式的解集为，则 的值为（　　　）

A．4　　　　　　  B．2　　　　　 C．　　　　　　 D．

9． 下列不是二元一次方程组的是（　　 ）

　　A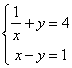．　　 B．　C．　　  D．

10．四个电子宠物排座位，一开始，小鼠、小猴、小兔、小猫分别坐在1、2、3、4号座位上（如图所示），以后它们不停地变换位置，第一次上下两排交换，第二次是在第一次换位后，再左右两列交换位置，第三次上下两排交换，第四次再左右两列交换……这样一直下去，则第2005次交换位置后，小兔子坐在（　　）号位上。

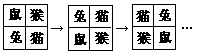　A．1　　B．2　　C．3　　D．4

二、看谁填得又对又准（本题共10个小题，每小题3分，共30分）

11．已知正多边形的内角和为1080°，那么这个正多边形的边数为　　　　　 ；又若正多边形的每一个外角都是72°，那么这个正多边形的内角和等于　　　　　　 。

12．周日，小华做作业时，把老师布置的一个正方形忘了画下来，打电话给小云，小云在电话中答复他：“你可以这样画，正方形ABCD的顶点A、B、C的坐标分别是（1，2）、（2，2）、（2，1），顶点D的坐标你自己想吧！”那么顶点D的坐标是　　　　　　　　 。

13．如图，BM是△ABC中AC边上的中线，AB = 5cm，BC = 3cm，那么△ABM与△BCM的周长之差为　　　　　　 。

14．在中，如果2= 6，那么=　　　 。

15．若有意义，则=　　　　 。

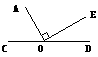
16．如图，∠COD为平角，AO⊥OE，∠AOC = 2∠DOE，则有∠AOC =　　　　　  。

　　

17、在去年足球甲A的前11轮（场）比赛中，某足球队保持连续不败记录，按比赛规则，胜一场得3分，平一场得1分，输一场计0分，若该队共积23分，那么该队共胜了　　场

18．如果，那么=　　　　  ，=　　　　　　 。

19．若等腰三角形的两边长分别为6cm和2cm，则它的周长为　　　　　　　　　 cm。

20、一玩具公司在每天工作10小时的机器上制造两种玩具：卫兵和骑兵，造一个卫兵需8秒和8克金属；造一个骑兵需6秒和16克金属，每天可供给的金属量最多只有64克，设造卫兵数x个，骑兵数为y个，那么x、y满足的关系式是　　　　　　　  。

三、计算能手——看谁既快又准（本题有4小题，共31分）

21（5分）已知F是⊿ABC的边BC的延长线上的一点，DF⊥AB于D，且∠A = 56°，

∠F = 31°，求∠ACB的度数。

　　　　　　 

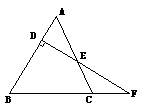
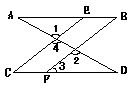
　　　　　 第21题图　　　　　　　　　  第22题图

22．（5分）如图，已知∠1 =∠2，∠B =∠C，可推得AB∥CD。理由如下：

　∵∠1 =∠2（已知），且∠1 =∠4（　　　　　  ）

∴∠2 =∠4（等量代换）

∴CE∥BF（　　　　　　　　　　　　  ）

∴∠　　 =∠3（　　　　　　　　　　 ）

又∵∠B =∠C（已知）

∴∠3 =∠B（等量代换）

∴AB∥CD（　　　　　　　　　　　 ）

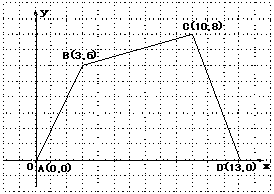
23．（5分）如图，在直角坐标系中，四边形ABCD各个顶点的坐标分别是A（0，0）、B（3，6）、C（10，8）、D（13，0），确定这个四边形的面积。你是怎样做的？

　

24、（16分）计算：

（1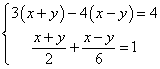）．　（2）已知，为何值时，不小于？

 

（2）一个正数x的平方根是2a3与5a，则a是多少？

（4）x²  = 0。

四、在数学中玩，在玩中学数学（本题有3小题，共19分）

25．（7分）中国象棋棋盘中蕴含着平面直角坐标系，如下图是中国象棋棋盘的一半，棋子“马”走的规则是沿“日”形的对角线走。例如：图①中“马”所在的位置可以直接走到点A、B处。

（1）如果“帅”位于点（0，0），“相”位于点（4，2），则“马”所在的点的坐标为　　　　  ，点C的坐标为　　　　 ，点D的坐标为　　　  。

（2）若“马”的位置在C点，为了到达D点，请按“马”走的规则，在图中画出一种你认为合理的行走路线，并用坐标表示。

　　　

26．（6分）〈〈一千零一夜〉〉中有这样一段文字：有一群鸽子，其中一部分在树上欢歌，另一部分在地上觅食，树上的一只鸽子对地上觅食的鸽子说：“若从你们中飞上来一只，则树下的鸽子就是整个鸽群的，若从树上飞下去一只，则树上、树下的鸽子就一样多了。”你知道树上、树下各有多少只鸽子吗？

27、（6分）甲、乙两件服装的成本共500元，商店老板为获取利润，决定将甲服装按50%的利润定价，乙服装按40%的利润定价，在实际出售时，应顾客要求，两件服装均按9折出售，这样商品共获利157元，求甲、乙两件服装的成本各是多少元？

五、数学探究与思考（本题共2小题，每小题10分，共20分）

28．观察并探求下列各问题，写出你所观察得到的结论，并说明理由。（每小题2分，观察得出结论与说明理由各占1分。）

（1）如图①，△ABC中，P为边BC上一点，试观察比较BP + PC与AB + AC的大小，并说明理由。

　

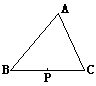
　　　　 图①

（2）将（1）中点P移至△ABC内，得图②，试观察比较△BPC的周长与△ABC的周长的大小，并说明理由。

　

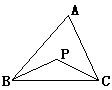
　　　　　 图②

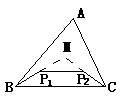
（3）将（2）中点P变为两个点P₁、P₂得图③，试观察比较四边形BP₁P₂C的周长与△ABC的周长的大小，并说明理由。

　　　　　　　　　　　　　　　　　　　　　 　 

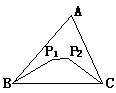
　　　　　 图③　　　　　　　　　　　　　　　　　　　　　　　　 图④

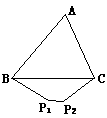
（4）将（3）中的点P₁、P₂移至△ABC外，并使点P₁、P₂与点A在边BC的异侧，且∠P₁BC＜∠ABC，∠P₂CB＜∠ACB，得图④，试观察比较四边形BP₁P₂C的周长与△ABC的周长的大小，并说明理由。

　　

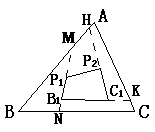
　 （5）若将（3）中的四边形BP₁P₂C的顶点B、C移至△ABC内，得四边形B₁P₁P₂C₁，如图⑤，试观察比较四边形B₁P₁P₂C₁的周长与△ABC的周长的大小，并说明理由。

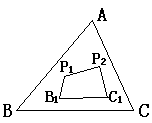
 图⑤

29、某校举行文艺节汇演，评出一等奖5个，二等奖10个，三等奖15个，学校决定给获奖

　的同学发奖品，同一等次的奖品相同，并且只能从下列所列物品中选取一件：

品名	小提琴	运动服	笛子	舞鞋	口琴	相册	笔记本	钢笔
单价（元）	120	8	24	22	16	6	5	4

（1）　　　 如果获奖等次越高，奖品单价就越高，那么学校最少要花多少钱买奖品？

（2）　　　 学校要求一等奖的奖品单价是二等奖品单价的5倍，二等奖的奖品单价是三等奖品单价的4倍，在总费用不超过1000元的前提下，有几种购买方案？花费最多的一种方案需要多少钱？

亲爱的同学，考试后进行反思是十分重要的，希望你能认真总结经验和不足，并将它写在笔记本上，这是你成长的记录，如果你对取得的成绩还感到不够满意，可以与老师联系，相信老师会根据你反思的情况，对你作出新的评价。

参考答案：

一、1、A　　 2、C　　3、B　　4、C　　5、D　　6、A　　 7、B　　　　　　　 

8、B　　 9、A　　10、A

二、11．8，540°　 12、（1，1）　 13、2cm　　14、1

　　　　15、1　　　　  16、60°　　　  17、6　　　18．3，2．

　　　　19、14cm　　　 20、8x+6y≤3600,8x+16y≤6400

三、21．65°　　　

22、对顶角相等；同位角相等，两直线平行；C；两直线平行，同位角相等；内错角相等，两直线平行。

23、32.5（提示：分别过A、B、C作x轴、y轴、x轴的平行线，将原图形补成一个矩形）

24、（1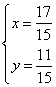） 　　 （2）m≥4　　（3）a =2　　 （4）x =±

四、25、（1）（3，0），（1，3），（3，1）　　　　　 （2）略

26、树上有7只，树下有5只。

27、300,200

五、28、25．（1）BP + PC＜AB + AC，理由：三角形两边之和大于第三边，或两点之间线段最短。

 （2）△BPC的周长＜△ABC的周长。理由：

如图，延长BP交AC于M，在△ABM中，BP + PM＜AB + AM，在△PMC中，PC＜PM + MC，两式相加得BP + PC＜AB + AC，于是得：△BPC的周长＜△ABC的周长。

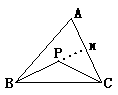
（3）四边形BP₁P₂C的周长＜△ABC的周长。理由：

　　如图，分别延长BP₁、CP₂交于M，由（2）知，BM + CM＜AB + AC，又P₁P_­2＜P₁M + P₂M，可得，BP₁ + P₁P₂ + P₂C＜BM + CM＜AB + AC，可得结论。

或：作直线P₁P₂分别交AB、AC于M、N（如图），△BMP₁中，BP₁＜BM + MP₁，△AMN中，MP₁ + P₁P₂ + P₂M＜AM + AN，△P₂NC中，P₂C＜P₂N + NC，三式相加得：BP₁ + P₁P₂ + P₂C＜AB + AC，可得结论。

　

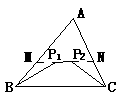
（4）四边形BP₁P₂C的周长＜△ABC的周长。理由如下：将四边形BP₁P₂C沿直线BC翻折，使点P₁、P₂落在△ABC内，转化为（3）情形，即可。

（5）比较四边形B₁P₁P₂C₁的周长＜△ABC的周长。理由如下：

如图，分别作如图所示的延长线交△ABC的边于M、N、K、H，在△BNM中，NB₁ + B₁P_­1 + P₁M＜BM + BN，又显然有，B₁C₁ + C₁K＜NB₁ +NC + CK，及C₁P₂ +P₂H＜C₁K +AK +AH，及P₁P₂＜P₂H + MH + P₁M，将以上各式相加，得B₁P₁ + P₁P₂ + P₂C + B₁C₁＜AB + BC + AC，于是得结论。

 

29、(1)根据题意得最少花费为6*5+5*10+4*15=140元

　 （2）设三等奖的奖品为x元，根据题意可得5*20x+10*4x+15x≤1000　,20x≤120 ,x≥4

 解得4≤x≤6

所以，方案1：三等奖奖品6元，二等奖奖品24元，一等奖奖品120元

　　　方案2：三等奖奖品5元，二等奖奖品20元，一等奖奖品100元（此方案不存在，舍去）

　　　方案3：三等奖奖品4元，二等奖奖品16元，一等奖奖品80元

所以购买方案有两种，其中花费最多为120*5+24*10+6*15=930（元）