成都七中实验学校2005~2006学年度下期期中考试
七 年 级 数 学(卷一)
A 卷(100分)
一、选择题(共30分.下列各小题只有一个正确答案,请你把它的序号填在卷二的表格中。)
1.下列计算正确的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.代数式![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中,单项式共有
中,单项式共有
(A) 1个 (B) 2个 (C) 3个 (D) 4个
3.一个多项式3a2-2b2减去一个多项式得3a2+2b2,则减去的多项式是
(A) -4b2 (B)4b2 (C)-6a2 (D) 6a2
4.成都至南充高速公路全程为260千米,它的百万分之一相当于
(A)你自己的身高 (B)一张课桌的长度
(C)数学期中考试卷的宽度 (D)黑板长度
5.下列各题的数,是准确数的是
(A)初一年级有527名同学 (B)月球离地球的距离为38万千米
(C)小明同学身高148cm (D)今天气温估计28℃
6.若(x-5)(x+2)= ![]() ,则p、q的值是
,则p、q的值是
A、3,10 B、-3,-10 C、-3,10 D、3,-10
7.下列能用平方差公式计算的是
(A)![]() (B)
(B) ![]()
 (C)
(C)![]() (D)
(D) ![]()
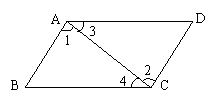
8.如图,由∠1=∠2,则可得出
(A) AD∥BC (B) AB∥CD
(C) AD∥BC且AB∥CD (D) ∠3=∠4
![]() 9.如图,
9.如图,![]() 与
与![]() 是对顶角的是
是对顶角的是
(A) 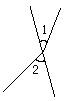 (B)
(B) 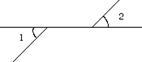 (C)
(C) 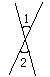 (D)
(D) 
10.转动下列各转盘,指针指向红色区域的概率最大的是( )
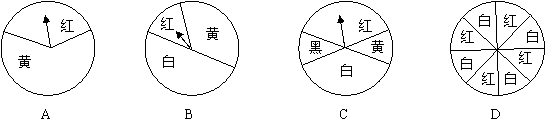 |
 成都七中实验学校2005~2006学年度下期期中考试
成都七中实验学校2005~2006学年度下期期中考试
七 年 级 数 学(卷二)
| 题号 | A 卷 | A卷 总分 | A 卷 | B卷 总分 | 全卷 总分 | |||||||
| 一 | 二 | 三 | 四 | 五 | 一 | 二 | 三 | 四 | ||||
| 得分 |
|
|
|
|
|
|
|
|
|
|
|
|
本试卷分为A卷和B卷,A卷满分100,B卷满分50分,全卷总分150分.考试时间120分钟
A 卷(100分)
一、选择题(每小题3分,共30分)
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 |
![]()
| |
| |
![]() 11.计算:(-2)0=______; (
11.计算:(-2)0=______; (![]() )-2=______.
)-2=______.
12.单项式 的系数是________;次数是________.
13.近似数![]() 有______个有效数字; 精确到
位.
有______个有效数字; 精确到
位.
 14.计算: (-2x2)3=________;
14.计算: (-2x2)3=________; ![]() .
.
15.计算: ![]() =
.
=
.
16.如图,∠AOC+∠DOE+∠BOF=
17.一个角与它的补角之差是20º,则这个角的大小是 .
18.一幅扑克去掉大小王后,从中任抽一张是红桃的概率是________.
19. 1根头发丝的直径为0.00006米,则利用科学记数法来表示,头发丝的直径是______________米.
20.如果多项式![]() 是一个完全平方式,则m的值是_________.
是一个完全平方式,则m的值是_________.
三、计算或化简求值(每小题5分,共20分)
21、
![]() 22、 9(x+2)(x-2)-(3x-2)2
22、 9(x+2)(x-2)-(3x-2)2
24.利用乘法公式计算:![]()
23.化简求值:![]() ,其中
,其中![]()
四.作图题(6分)
25.已知:线段AB,
![]()
求作:线段A′B′,使A′B′=AB.
 作法:(1)作射线A′C′;
作法:(1)作射线A′C′; ![]()
(2)以点_____为圆心,以_______为
半径画弧交A′C′于点B′;
_________就是所作的线段.
26.已知:![]() 及AB边上一点D,
及AB边上一点D,
过点D画BC的平行线.
(尺规作图,不写作法,保留作图痕迹).
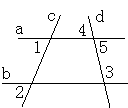 五、(27题4分,28、29题各5分.共14分)
五、(27题4分,28、29题各5分.共14分)
27.阅读下列推理过程,在括号中填写理由:
已知:如图,∠1=∠2.试说明∠3+∠4=180°
解:∵∠1=∠2 ( 已知)
∴ a∥b ( )
∴∠3+∠5=180°( )
又∵∠4=∠5 ( )
∴∠3+∠4=180°( )
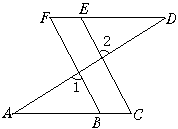
28.如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
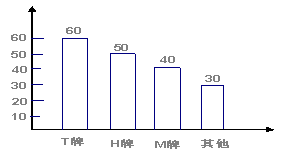
29.如图所示为某个月中不同牌子的私家小汽车的销量统计.
(1)M牌的销量占总销量的百分比是_______.
(2)利用一象形图表示这些数据.
B 卷 (50分)
一、填空题(每题4分,共32分)
30.小颖看小明是北偏东30°,那么小明看小颖时,它的方向是
31.将一个各面涂有颜色的正方体,分割成同样大小的27个小正方体,从这
 些正方体中任取一个,恰有3个面涂有颜色的概率是__________.
些正方体中任取一个,恰有3个面涂有颜色的概率是__________.
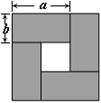
32.如图是用四张相同的长方形纸片拼成的图形,
请利用图中空白部分的面积的不同表示方法写出
一个关于a、b的等式 _______________
33.若![]() ,则
,则![]() 的值为___________.
的值为___________.
34.若(x2+mx)(x2-3x+1)的积中不含x3的项,则m的值是 ______
35.已知∠1的两边分别平行∠2的两边,∠2=500,则∠1的度数为__________。
36.已知:3a2+3a=1,则6a4+15a3+10a2+2005的值为________.
37.已知:直角三角形的两条直角边的和是4,平方和是14,则它的面积是_____.
二.(6分)
38.如图16,已知∠1=∠2,∠C=∠F,请问∠A与∠D存在什么关系?验证你的结论.
三.(本题6分)
39. 如图是2003年12月份的日历牌,我们在日历牌中用两种不同的方式选择四个数。
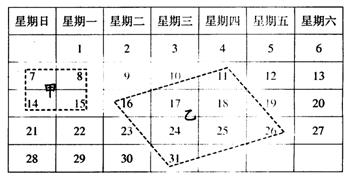
(1)从甲种选择构成的“矩形”中发现14×8-7×15=7,即对角线上两数积的差为7。请你平行移动矩形甲,使它的四个顶点落在其他的四个数上,对角线上的两数积的差为_________.
(2)对乙种选择构成的“平行四边形”顶点处的四个数字,按上述方法计算和平移,你得出的结论是__________________________________.
(3)由(2)小题得出的这些规律是否具有一般性?如果你认为不具有一般性,请举反例;如果你认为具有一般性,请假设所选择的某个数为n,然后通过含n的代数式的运算加以说明。
四、(本题6分)
40. 概率论起源于赌博,据传意大利的业余数学家卡当就曾热衷于赌博,试图研究赌博不输的方法。卡当曾参加过这样一次赌博:把两个骰子掷出去,以每个骰子朝上的点数之和作为赌的内容,那么你认为卡当把赌注下在几点最有利呢?并说明理由。