重庆市商务学校2005-2006学年度（下）第三次月考
七 年 级 数 学 试 题
| 得分 | 评卷人 |
（全卷共四大题，满分150分，120分钟完卷）
一、选择题（每小题4分，共40分）
1、下列语句中错误的是 （ ）.
A．数字 0 也是单项式 B．单项式 a 的系数与次数都是 1
C．
x2 y2是二次单项式
D．
的系数是
2、若
，则
、
的值分别为（
）.
A．
，
B．
，
C．，
D．，
3、一个长方体的长、宽、高分别是
、
、
，它的体积等于（ ）.
A．
B．
C．
D．
4、据国家商务部消息，2005年一季度，我国进口总额达2952亿美元．用科学记数法表示这个数是（ ）
A．2.952×10
亿美元
B．0.2952×10
亿美元
C．2.952×10亿美元
D．0.2952×10
亿美元
5、下列事件一定为必然事件的是（ ）
A．重庆人都爱吃火锅； B．某校随机检查20名学生的血型，其中必有A型
C．内错角相等，两直线平行；D．在数轴上，到原点距离相等的点所表示的数一定相等
6、设(5a＋3b)＝(5a－3b)＋A ，则A＝(
)
A.30ab B.60ab C.15ab D.12ab
7、已知变量x、y满足下面的关系:
| x | …… | -3 | -2 | -1 | 1 | 2 | 3 | …… |
| y | …… | 1 | 1.5 | 3 | -3 | -1.5 | -1 | …… |
则x、y之间用关系式表示为( )
A.y=
B.y=－
C.y=－ D.y=
8、如图，下列条件中，不能判断直线l1∥l2的是（ ）
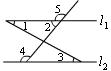A、∠1=∠3 B、∠2=∠3
C、∠4=∠5 D、∠2+∠4=180°
9、.如图，△ABC中，∠C=
，AC=BC，AD是△ABC的角平分线，DE⊥AB于E，若AB=6
，则△DEB的周长为（ ）
A.5
B.6
C.7
D.8
10、下列说法中，正确是个数有（ ）个
（1） 两个角和一边相等的两个三角形全等
（2） 两条边和其中一条边的对角对应相等的两个三角形全等。
（3） 有一条边相等的两个等边三角形全等。
（4） 近似数2.4万有两个有效数字，精确到十分位。
（5） 三角形的最大角不小于
。
A 1 B 2 C 3 D 4
| 得分 | 评卷人 |
二、填空题（每小题3分，共30分）
11、已知
，则
.
12、若
，则＝____________
13、若∠α与∠β互补，且∠α︰∠β＝5︰4，则∠α－∠β＝________.
14、小红上学共要路过三个十字路口,每个路口都有红绿灯,她在每个路口遇到红灯的概率都是0.5,则她从家到学校一路通行的概率是________.
15、2000年对10万人受教育程度的统计结果表明，高中或高中以上学历人数为14757人，精确到千位可写为 .
16、等腰三角形两边长分别为3、6，则其周长为 .
17、如图所示，∠α = 度。
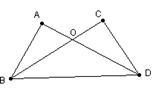
18、如图，已知∠A =∠C，要证明⊿AOB≌⊿COD,根据“ASA”还要一个条件__________。
 |
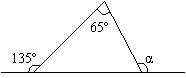（17题） （18题）
19、用边长60cm的正方形铁皮做一个无盖水箱,先在四个角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成,如果截去的小正方形的边长是xcm,水箱的容积是ycm3,则因变量y与自变量x之间的关系式是_____ ____.
20、
一圆锥高为6cm，当其底面半径从5cm变化到10cm时, 其体积从 变化到
(保留π)
| 得分 | 评卷人 |
三、解答题(本大题共4小题，共38分)
21、计算（每小题4分，共12分）
(1)
(2) 
（3）用乘法公式计算：
22、（本题8分）
，其中
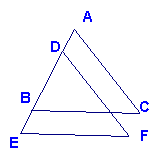23（本题8分）已知：如图BC∥EF，BC=EF，AB=DE；说明ＡＣ与ＥＦ相等。
解：∵BC∥EF（已知）
∴∠ABC=∠__________（ ）
在△ABC和△DEF中
______=_______
∵ _______=________
______=________
∴△ABC≌___________ ( )
∴ AC=DF ( )
24、探索题（本题10分）
（1）如图1，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C．△ABC中，∠A＝30°，则∠ABC＋∠ACB＝ 度，∠XBC＋∠XCB＝ 度；
（2）如图2，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C，那么∠ABX＋∠ACX的大小是否变化？若变化，请举例说明；若不变化，请求出∠ABX＋∠ACX的大小．
（图1） （图2）
| 得分 | 评卷人 |
四、解答题。（本大题共4小题，25、26、27每题10分， 28题12分，共42分）
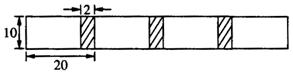
25（本题10分） 将若干张长为20cm、宽为10cm的长方形白纸，按下图所示的方法粘合起来，粘合部分的宽为2cm．
（1）求4张白纸粘合后的总长度；
（2）设x张白纸粘合后的总长度为ycm，写出y与x之间的关系式，并求当x＝20时，y的值
26、 （本题10分）如图， 货车和轿车先后从甲地出发，走高速公路前往乙地. 下图表示行驶过程中，他们的行驶路程（千米）与所用时间（分钟）的关系的图象. 已知全程为90千米，根据图象上的信息回答问题
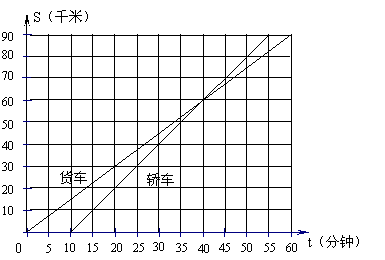
（1）、货车比轿车早 分钟从甲地出发；轿车到达乙地 分钟后货车才到；
（2）、轿车开出 分钟后追上货车
（3）、分别求出货车和轿车的速度。
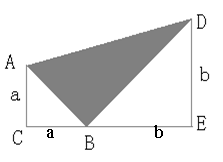
27. （本题10分）已知：两个等腰直角三角形（
）边长分别为a和b（
）如图放置在一起，连接AD，
（1） 求阴影部分(
)的面积（4分）
（2） 如果有一个
点正好位于线段
的中点，连接
、
得到
,求的面积（4分）
（3） 
（2）中的三角形比（1）中的面积大还是小？（2分）
28、（本题12分）.已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,
（1）与
全等吗？请说明理由。
（2）判断BD与DE+CE关系，并请说明理由。
