二OO六年春七年级数学第五、六章检测题
（时间：120分钟 满分：120分） 总分：
一、选择题（每小题2分，共30分）
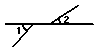
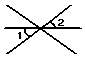
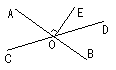
1．下面四个图形中，∠1与∠2是对顶角的图形的个数是（ ）
A．0 B．1 C．2 D．3
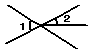
2．一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐弯的角（ ）
A．第一次右拐50°，第二次左拐130°。B．第一次左拐50°，第二次右拐50°。
C．第一次左拐50°，第二次左拐130°。D．第一次右拐50°，第二次右拐50°。
3．同一平面内的四条直线满足a⊥b，b⊥c，c⊥d，则下列式子成立的是（ ）
A．a∥b B．b⊥d C．a⊥d D．b∥c
4．三条直线两两相交于同一点时，对顶角有m对,交于不同三点时，对顶角有n对，则m与n的关系是（ ）
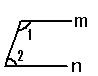A．m = n B．m＞n C．m＜n
D．m +
n = 10
5．如图，若m∥n，∠1 = 105°，则∠2 =（ ）
A．55° B．60° C．65° D．75°
6．下列说法中正确的是（ ）
A．有且只有一条直线垂直于已知直线。 （第5题图）
B．从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离。
C．互相垂直的两条直线一定相交。
D．直线c外一点A与直线c上各点连接而成的所有线段中，最短线段的长是3cm，则点A到直线c的距离是3cm。
7．如图示，直线a、b都与直线c相交，下列条件中，能说明a∥b的是（ ）
①∠1=∠2；②∠2=∠8；③∠2=∠8；④∠1+∠4=180°
A、①② B、①②③ C、①②④ D、①②③④
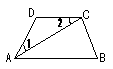
8．如图所示，已知AD∥BC，BD平分∠ABC，且∠A：∠ABC=2：1，则∠ADB等于（ ）
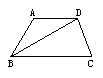A．300 B．450 C．600
D．700
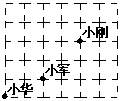
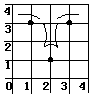
9．课间操时，小华、小军、小刚的位置如图，小华对小刚说，如果我的位置用
（0，0）表示，小军的位置用（2，1）表示，那么你的位置可以表示成（ ）
A．（5，4） B．（4，5） C．（3，4） D．（4，3） （第8题图）
|
（第7题图） （第9题图） （第10题图）
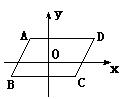
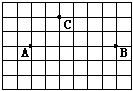
10．如图，下列说法正确的是（ ）
A． A与D的横坐标相同。 B． C与D的横坐标相同。
C． B与C的纵坐标相同。 D． B与D的纵坐标相同。
11．若x轴上的点P到y轴的距离为3，则点P的坐标为（ ）
A．（3，0） B．（3，0）或（–3，0） C．（0，3） D．（0，3）或（0，–3）
12．如果点P（5，y）在第四象限，则y的取值范围是（ ）
A．y＜0 B．y＞0 C．y≤0 D．y≥0
13．线段CD是由线段AB平移得到 的。点A（–1，4）的对应点为C（4，7），则点B（– 4，– 1）的对应点D的坐标为（ ） A．（2，9） B．（5，3） C．（1，2） D．（– 9，– 4）
14．一个长方形在平面直角坐标系中三个顶点的坐标为（– 1，– 1）、（– 1，2）、（3，– 1），则第四个顶点的坐标为（ ） A．（2，2） B．（3，2） C．（3，3） D．（2，3）
15．点A、B关于x轴的对称，已知点A的坐标为（5，-2）则点A的坐标为( )
A （5，2） B （-5，2） C （-5，-2） D （-2，-5）
二、填空题（每小题3分，共30分）
1．命题：若两个角的和是180°，则这两个角互补。题设是： ，结论是： 。
2．猜谜语（打本章两个几何名称）。剩下十分钱 ；两牛相斗 。
3．下面生活中的物体的运动情况可以看成平移的是 。
（1） 摆动的钟摆。 （2）在笔直的公路上行驶的汽车。（3）随风摆动的旗帜。
（4）摇动的大绳。 （5）汽车玻璃上雨刷的运动。 （6）从楼顶自由落下的球（球不旋转）。
|
|
|
|
|
（第4题图） （第5题图） （第7题图） （第10题图）
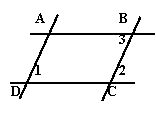5．如图，AC平分∠DAB，∠1 =∠2。填空：因为AC平分∠DAB，
所以∠1 = 。所以∠2 = 。所以AB∥ 。
6、如图，若∠2=∠3，则根据 可得
若∠2=∠1，则根据 ，可得
如果AD∥BC，那么根据 可得
如果AB∥CD，那么根据 可得
7．如图是小刚画的一张脸，他对妹妹说“如果我用（1，3）表示左眼，用（3，3）表示右眼，那么嘴的位置可以表示成 。
8．点A在x轴上，位于原点的右侧，距离坐标原点5个单位长度，则此点的坐标为 ；点B在y轴上，位于原点的下方，距离坐标原点5个单位长度，则此点的坐标为 ；点C在y轴左侧，在x轴下方，距离每个坐标轴都是5个单位长度，则此点的坐标为 。
9．小华将直角坐标系中的猫的图案向右平移了3个单位长度，平移前猫眼的坐标为（– 4，3）、（– 2，3），则移动后猫眼的坐标为 。
10．如图，小强告诉小华图中A、B两点的坐标分别为（– 3，5）、（3，5），小华一下就说出了C在同一坐标系下的坐标 。
三、算一算（每小题6分，共12分）
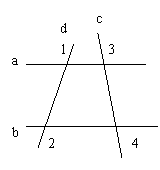
1. 如图，AD是∠EAC的平分线，AD∥BC，∠B = 30°，
你能算出∠EAD、∠DAC、∠C的度数吗？
 |
2. 如图, ∠1=∠2 , ∠3=1050， 求 ∠4的度数。
四、想一想、将下列解题过程补充完整。（每空1分，共14分）
1．如图，EF∥AD，∠1 =∠2，∠BAC = 70°。将求∠AGD的过程填写完整。
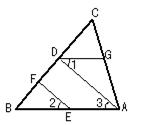因为EF∥AD，所以 ∠2 =
。
又因为 ∠1 = ∠2，所以 ∠1 = ∠3。
所以AB∥ 。
所以∠BAC + = 180°。
又因为∠BAC = 70°，
所以∠AGD = 。
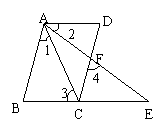2．已知，如图，BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4。
AD与BE平行吗？为什么？。
解：AD∥BE，理由如下：
∵AB∥CD（已知）
∴∠4=∠ （ ）
∵∠3=∠4（已知）
∴∠3=∠ （ ）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF（ ）
即∠ =∠
∴∠3=∠ （ ）
∴AD∥BE（ ）
五、画一画 （每小题5分，共12分）
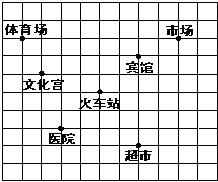
1.如图，这是某市部分简图，请以火车站为坐标原点建立平面直角坐标系，并分别写出各地的坐标。
2 请建立适当的直角坐标系，并描出A（– 3，– 2）、
B（2，– 2）、C（– 2，1）、D（3，1）四个点，
线段AB、CD有什么关系？顺次连接A、B、
C、D四点组成的图形是什么图形？
六、试一试（每小题7分，共14分 ）
1． 
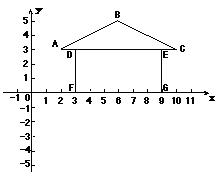如图，（1）请写出在直角坐标系中的房子的A、B、C、D、
E、F、G的坐标。（2）源源想把房子向下平移3个单位长度，
你能帮他办到吗？请作出相应图案，并写出平移后的7个点
的坐标。
2．.如图(10),∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
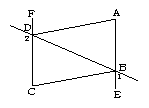(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么. ?
七、做一做（每小题4分，共8分）
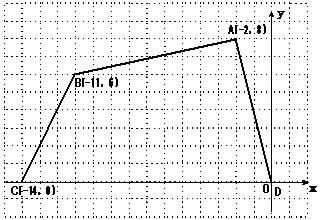
1. 如图，四边形ABCD各个顶点的坐标分
（– 2，8），（– 11，6），（– 14，0），（0，0）。
①确定这个四边形的面积，你是怎么做的?
②如果把原来ABCD各个顶点纵坐标保持
不变，横坐标增加2，所得的四边形面积又
是多少？
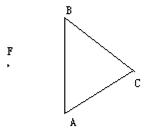
2． 已知三角形ABC、点C平移后到点F，
作出三角形ABC平后的三角形DEF。