2006年春七年级数学单元测试卷---《轴对称》
班级 座号 姓名 得分
一、耐心填一填(3’×10 = 30’)
1、线段的对称轴有 条。
2、角是轴对称图形,它的对称轴是__________________________.
3、下面是我们熟悉的四个交通标志图形,请从几何图形的性质考虑,哪一个与其他三个不同?请指出这个图形,并说明理由。

答:这个图形是: (写出序号即可),理由是 。
4、底角等于顶角一半的等腰三角形是___________三角形.
5、线段的 上的点到这条线段两个端点的距离相等。
6、如果等腰三角形的顶角为70°,那么它的一个底角为_______.
 7、若点P在∠BAC的平分线上,它到AB的距离为3cm,
7、若点P在∠BAC的平分线上,它到AB的距离为3cm,
则它到AC的距离为________cm.
8、已知等腰三角形的一边为3㎝,另一边长为7㎝,
则它的周长为 ㎝。
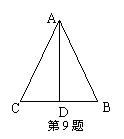
9、如图,△ABC中,AD垂直平分边BC,且
 △ABC的周长为24,则AB+BD = .
△ABC的周长为24,则AB+BD = .
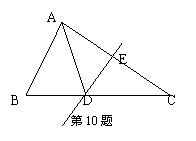
10、如图,![]() ABC中,AC的垂直平分钱交AC于E,
ABC中,AC的垂直平分钱交AC于E,
交BC于D,![]() ABD的周长为12,AE=5,
ABD的周长为12,AE=5,
则![]() ABC的周长为_____.
ABC的周长为_____.
二、精心选一选(4’×6= 24’)
11、如图,下列图案是我国几家银行的标志,其中是轴对称图形的有( )
A、1个 B、2个 C、3个 D、4个
12、等腰三角形中的一个角等于100°,则另两个内角的度数分别为( )
A、40°,40° B、100°,20°
C、50°,50° D、40°,40°或100°,20°
13、下列轴对称图形中,对称轴最多的是( )。
A、等腰直角三角形
B、有一角为![]() 的等腰三角形
的等腰三角形
C、正方形 D、圆
14、已知△ABC中,AB=AC,且∠B =θ,则θ的取值范围是( )
 A、θ≤45°
B、0°<θ<90°
A、θ≤45°
B、0°<θ<90°
C、θ=90° D、90°<θ<180°
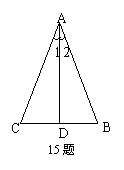
15、如图,在已知△ABC中,AB=AC,BD=DC,
则下列结论中错误的是( )
A、∠BAC=∠B B、∠1=∠2
C、AD⊥BC D、∠B=∠C
16、以下叙述中不正确的是( )
A、等边三角形的每条高线都是角平分线和中线
B、两个对称图形对应点连线的交点一定在它们的对称轴上
C、点A,B可以看作以直线AB为轴的轴对称图形
D、若A、A′是以BC为轴对称点,则AA′垂直平分BC
三、认真画一画(3’+6’ +6’)
17、用直尺和量角器在下图中的直线AB上找一点M,使ME = MF。
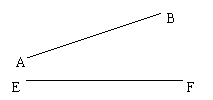 |
![]()
![]() 18、用两个圆:○、○,两个三角形:△、△,和两条线段: 、 ,拼出至少两个对称图形(画在以下方框内)。
18、用两个圆:○、○,两个三角形:△、△,和两条线段: 、 ,拼出至少两个对称图形(画在以下方框内)。
 |  |
19、画下列图形关于直线MN的对称图形.
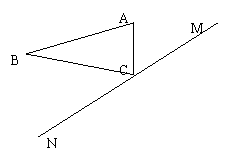 |
四、细心算一算(10’+10’)
20、如图,在△ABC中,AB=AC,∠BAC=100°,AD⊥BC,
垂足为D,求∠B,∠C,∠BAD,∠CAD的度数.
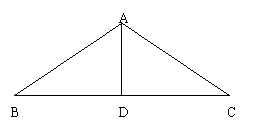 |
21、如图,在△ABC中,∠ABC =2∠C,BD平分∠ABC,DE⊥AB(E在AB之间),DF⊥BC,已知BD=5,DE=3,CF=4。试求△DFC的周长。
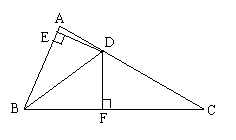
五、决心试一试(11’)
22、如图,AB=AC=CD,AB∥CD,AD与BC相交于O点,
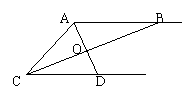 问:BC与AD是否垂直?为什么?
问:BC与AD是否垂直?为什么?
参考答案:
一、1、2 2、角平分线所在的直线 3、 (2) 其它三个都是轴对称图形 4、等腰直角 5、垂直平分线 6、55° 7、3 8、17
9、12 10、22
二、C A DBAD
三、(略)
四、20、解:∵∠B+∠C+∠BAC=180°,∠BAC =100°
∴∠B+∠C= 80°
∵AB=AC
∴∠B =∠C= 40°
∵AB=AC,AD⊥BC
∴∠BAD =∠CAD=![]() ∠BAC= 50°
∠BAC= 50°
21、解:∵BD平分∠ABC,DE⊥AB, DF⊥BC
∴DE = DF,∠DBC = ![]() ∠ABC
∠ABC
又∵∠ABC =2∠C
∴∠DBC =∠C,∴BD = CD
∵BD=5,DE=3,CF=4
∴△DFC的周长=DF+DC+CF=DE+BD+CF=12
22、解:BC⊥AD
理由:∵AB=AC
∴∠ACB=∠ABC
∵AB∥CD
∴∠ABC=∠BCD
∴∠ACB=∠BCD
∵AC=CD
∴BC⊥AD