浙教版七上第四章代数式难题集萃
1．小红家9月份用了
度电，10月份比9月份节约了
度电，已知每用一度电须缴电费
元，则小红家10月份应缴电费________元.
2.一辆汽车有甲地以每小时65千米的速度驶向乙地,行驶3小时即可到达乙地,则在行驶
小时后离甲地________千米,距乙地______千米.
3.随着计算机技术的迅速发展,电脑价格不断降低,某品牌电脑按原价降价20%,现售价为
元,那么该电脑的原价为________元.
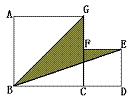4.如图,正方形ABCG和正方形CDEF的边长分别为
,用含的代数式表示阴影部分的面积。
5、一种空调2月份售价是元，5月份售价上浮10%，10月份又比5月份下调10%.
（1）用代数式分别表示5月份和10月份的售价；
（2）几月份去购买这种空调比较便宜？为什么？
6、已知
求代数式
的值。
7、已知
，则
__________
8、已知
，则
=________
9、已知代数式
的值等于8，那么代数式
_______
10、已知
，那么代数式
________
11、当
时，代数式
的值为2005，则当
时，代数式的值为___________
12、某市出租车收费标准为：起步价6元（即行驶距离不超过3km都付6元车费），超过3km后，每增加1km，加收2.4元（不足1km按1km计算）。某人乘坐了
km（为大于3的整数）路程。
（1）试用代数式表示他应付的费用；
（2）求当
时的乘车费用；
（3）若此人付了30元车费，你能算出此人乘坐的最远路程吗？
13、一个五次多项式，它的任何一项的次数（ ）
A．都小于5 B．都等于5 C．都不大于5 D．都不小于5
14、如果
是关于
的五次单项式，则常数
满足的条件是（ ）
A．
B．
C．
D．
15、已知
是关于的单项式，且系数为
，次数是4，求代数式
的值。
16、观察下列单项式：
，你能写出第个单项式吗？并写出第2005个单项式。
为了解决这个问题，我们不妨从系数和次数两个方面入手进行探索，从中发现规律，经过归纳猜想结论。
（1） 系数规律有两条：
① 系数的符号规律是________; ②系数的规律是________.
(2)次数的规律是___________;
(3)根据上面的归纳，可以猜想第个单项式是__________;
(4)根据猜想的结论，第2005个单项式是___________.
17.已知多项式
是六次四项式，单项式
的次数与多项式的次数相同，求
的值。
18.已知
与
是同类项，则等于（ ）
A．4 B．37 C．2或4 D．2
19．若
，则
_______
20请写出
的两个同类项，且这两个同类项与合并后为0，你给出的两个同类项
为__________
21.如果关于字母的多项式
的值与的取值无关，求的值。
22.已知
，化简：
=________
23．化简：
=________
24．已知长方形的周长是
，长是
，则宽是______________
答案：
１、
２、６５ｔ １９５－６５ｔ
３、1.25n
4、
5、1.1a 10
6、
7、1
8、9
9、2
10、-4.5
11、-2003
12、2.4x-1、2 18 13
13、C
14、B
15、 6.5 或 3.5
16、略
17、-1
18、D
19、11
20、略
21、m=1 n=3
22、 0
23、 9a-10b
24、0.5a+b