相交线与平行线检测题（1）
姓名： 班级：
一、判断题 20分（正确填A错误填B）
1. 同一平面内，两条不同直线有平行、相交、垂直三种位置关系（ ）
2. 同位角相等 （ ）
3. 两边互为反向延长线的两个角叫做对顶角 （ ）
4. 有一条公共边，另一边互为反向延长线的两个角叫做邻补角（ ）
5. 邻补角的角平分线互相垂直 （ ）
6. 直线外一点到这条直线的垂线段的长度叫做点到直线的距离（ ）
7. 任意用一条直线截两条平行直线，截得的同位角相等，内错角相等，同旁内角互补（ ）
8. 同一平面内，垂直于同一直线的两直线平行（ ）
9. 平行于同一直线的两直线平行（ ）
10.
|
二、
|
|
|
|
|
|
A.
|
|
 |
12.
|
|
|
A. 90° B.15° C.60° D.30°
13. 两边分别平行的两个角的大小关系是 （ ）
|
|
|
|
|
14．如图3,由DC∥AB,可得 ( )
A. ∠DCA=∠CAB B. ∠DAC=∠ACB
C. ∠DCA=∠CAB和∠DAC=∠ACB D. DA∥CB
|
|
|
|
|
|
|
|
15．如图4,∠1=∠2=110°, ∠3=120°则∠4= ( )
|
|
|
|
|
16. 如图5，四边形ABCD中，AE⊥DC,BF⊥DC,三角形ADC与
三角形BDC的面积相等，则下面结论正确的个数是（ ）
（1） AE=BF
（2） AB∥DC
（3） 线段AE的长度是点A到DC的距离
（4）
|
|
|
17. 两条直线交于一点，下面说法正确的个数是（ ）
A. 构成2对对顶角
B. 没有同位角
C. 有4对邻补角
D. 同角的邻补角是对顶角
A. 1 B. 2 C. 3 D. 4
18．下面语句是命题是（ ）
A. 画线段AB=CD.
B.
∠1与∠2相等吗？
C. 对顶角相等.
D. 过点A作CD∥EF.
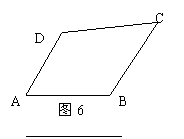
19. 如图6, 四边形ABCD中AD∥BC，则互补的角有（ ）对
A. 1 B. 2 C. 3 D. 4
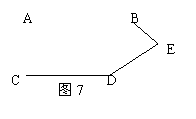
20. 如图7. AB∥CD,则∠B, ∠D, ∠E有下面的关系 （ ）
A. ∠B+∠D+∠E=360°
B. ∠B+∠D+∠E=720°
C. ∠B+∠D+∠E=180°
D. 无法确定
答题卡
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
三、填空题 12分
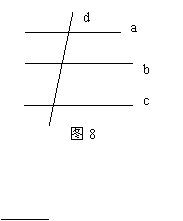
21．如图8, 用数字在图中标出需要的角，然后写出
当
或
时，a∥b
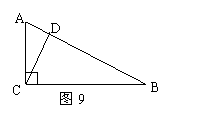
22. 如图9, AC⊥CB, CD⊥AB,则
是点A到BC的垂线段
是点B到DC的垂线段
是点C到AB的垂线段
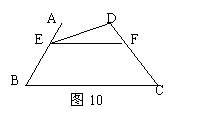23. 如图10， 完成下面推理过程并写出理由
∵∠ADE=∠DEF(已知)
∴AD∥ (
)
∵∠EFC+∠C=180°(已知)
∴EF∥ (
)
∴ ∥ (
)
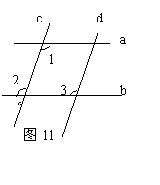
24．如图11，已知a∥b，c∥d ，∠1=115°求 ∠2，∠3
解：∵a∥b(已知)
∴∠2=∠1=115°( )
∵c∥d (已知)
∴∠3=∠2=
（
）
四、解答题
25 按下面语句画图
1． 
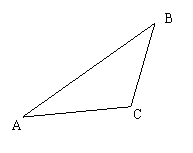画垂线CD⊥AB,垂足为D；
2． 过点B画AC的垂线段, 垂足为E；
3． 过点A画BC的平行线，交CD于F。
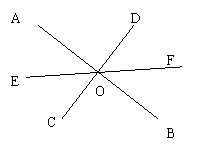26直线AB、CD、EF交于点O,如果EF平分∠AOC
EF平分∠BOD吗？为什么？
27．如图12，已知：AB∥CD,试再添上一个条件使∠1=∠2。（要求给出两个以上的答案）
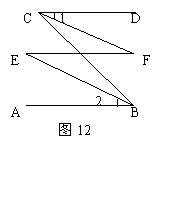并就其中一个说明理由。
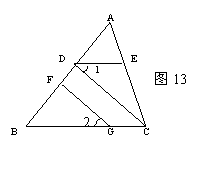
28如图13，AB⊥DC, GF⊥AB, D、F为垂足。G在BC上∠1=∠2。
请判断DE与BC的位置关系并说明理由。
 |
相交线与平行线测试题（2）
姓名： 班级：
一、选择题（共6小题，每小题3分，共18分）
下列各题中均有四个备选答案，其中有且只有一个是正确的，请将正确答案的代号填在题后的括号内．
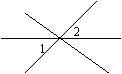
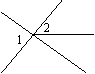
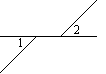
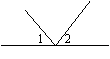
1．下面四个图形中，∠1与∠2是对顶角的图形有( )．
（A） 0个 （B）1个 （C）2个 （D）3个
2．一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐弯的角度是( )．
（A）第一次右拐50°，第二次左拐130° （B）第一次左拐50°，第二次右拐50°
（C）第一次左拐50°，第二次左拐130° （D）第一次右拐50°，第二次右拐50°
3．同一个平面内的四条直线若满足a⊥b，b⊥c，c⊥d，则下列式子成立的是( )．
（A）a∥d （B）b⊥d （C）a⊥d （D）b∥c
4．三条直线两两相交于同一点时，对顶角有m对；交于不同三点时，对顶角有n对，则m与n的关系是( )．
（A）m=n （B）m＞n （C）m＜n （D）m+ n =10
5．如图，若m∥n，∠1=105°，则∠2= ( )．
（A）55°（B）60°（C）65°（D）75
6．下列说法中正确的是 ( )．
（A） 有且只有一条直线垂直于已知直线
（B） 从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离
（C） 互相垂直的两条线段一定相交
（D）直线c外一点A与直线c上各点连接而成的所有线段中最短线段的长是3cm，则点A到直线c的距离是3cm
二、填空题（共5小题，每小题3分，共15分）
7．两个角的两边两两互相平行，且一个角的
等于另一个角的
，则这两个角的度数分别是
.
8．猜谜语（打两个几何角的名称）剩下十分钱： ；
两牛相斗： .
9．下面生活中的物体的运动情况可以看成平移的是 .
（1）摆动的钟摆；（2）在笔直的公路上行驶的汽车；（3）随风摆动的旗帜；（4）摇动的大绳；（5）汽车玻璃上雨刷的运动；（6）从楼顶自由落下的球（球不旋转）.
10．如图，直线AB、CD相交于点O，O为垂足，如果∠EOD=38°，则∠AOC= ，∠COB= .
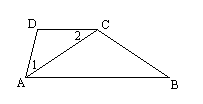11．如图，AC平分∠DAB，∠1=∠2.填空：因为AC平分∠DAB，所以∠1=
.所以∠2= .所以AB∥
.
三、做一做（本题4分）
12．已知三角形ABC、点D，过点D作三角形ABC平移后的图形，使A的对应点为D.
(保留作图痕迹)
四、算一算（本题5分）
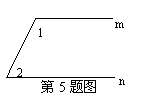
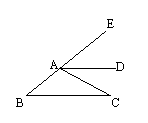13．如图，AD是∠EAC的平分线，AD∥BC，∠B=30°，你能算出∠EAD、∠DAC、∠C的度数吗？
五、想一想（括号中填写根据；每空2分，共48分）
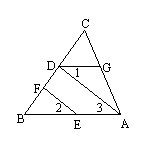14．如图EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．
证明：∵EF∥AD
∴∠2= （ ）.
又∵∠1=∠2，∴∠1=∠3.
∴AB∥ （ ）.
∴∠BAC+ =180°.（ ）
∵∠BAC=70°，
∴∠AGD= .
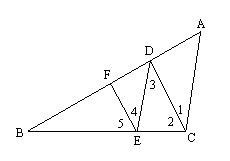
15．如图,已知AC∥DE,DC∥FE,CD平分∠ACB. 求证:EF平分∠BED．
证明: ∵AC∥DE
∴∠1=∠3 ( )
又 ∵CD平分∠ACB
∴_____ = ____（ ）
∴∠2 = _________
∵DC∥FE
∴∠5=_____ ( )
∠4=_____ ( )
∴∠4=∠5
即EF平分∠BED（ ）
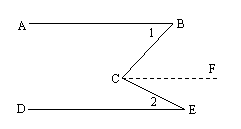
16．已知：如图，∠BCE=∠1+∠2，试说明AB∥DE
解：过C点作AB的平行线CF.
则∠1= ，（ ）
又∵∠BCE=∠1+∠2，（ ）
∴∠2=∠FCE（等量减等量差相等）
∴ ∥ （ ）
∴AB∥CD（ ）
六、试一试（本题5分）
17．在同一个平面内（1）已知三条不同的直线a1、a2，a3，且a1⊥a2，a2⊥a3.请问a1与a3有什么位置关系？为什么？(2分)
（2）已知十条不同的直线a1、a2，……a9、a10，且a1⊥a2，a2⊥a3，a3⊥a4，a4⊥a5，a5⊥a6，a6⊥a7，a7⊥a8，a8⊥a9，a9⊥a10.请问a1与a10有什么位置关系？为什么？（2分）
（3）在你探究上题的过程中，有什么规律，有什么发现？写下来.（2分）
七、拓展资源（本题5分）
18．如图 , AB∥CD,∠1=∠B, ∠2=∠D.运用平行线的知识说明BE⊥DE.
解：