初一数学期末考模拟卷
姓名： 班别： 学号： 成绩：
一、选择题：（本大题共10小题，每小题2分，共20分．在每小题给出的四个选项中，只有一项是符合题目要求的，将答案填在下面的答题卡上）．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1．下列方程中，是一元一次方程的是（ ）．
A．
B.
C．
D．
2．如果
是方程
的一个解，那么k的值是（ ）．
A．
B．
C．2
D．4
3．已知关于x 的方程
与
的解相同，则k＝（ ）
A．7 B．-8 C．9 D．－10
4．以下各组数据为长度的三条线段，能组成三角形的是（ ）．
A．1，2，3 B．1，4，3 C．5，9，5 D．2，7，3
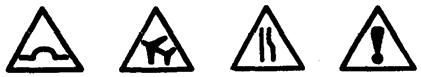5．如图所示，下列图形中，轴对称图形的个数有( )
A．4个 B．3个 C．2个 D．1个
6．若等腰三角形的周长为10，一边长为4，则此等腰三角形的腰长为（ ）
A．2 B．3 C．4 D．3或4
7．下列事件中，必然发生的是（ ）
A．期末考试数学得满分 B．如果两个解是对顶角，则这两个角相等
C．今天刮风了，明天会下雨
D．如果
，则a＝b
8．若用一种正多边形瓷砖铺满地面，则这样的正多边形可以是（ ）
A．正三、四、六边形 B．正三、四、五边形
C．正三、四、五、六边形 D．正三、四、六、八边形
9．（n＋1）边形的内角和比n边形的内角和大（ ）
A．180° B．360° C．
D.
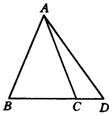
10．在△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC交AC于D，则图中共有等腰三角形的个数为（ ）
A．1个 B．2个 C．3个 D．不确定
二、填空题：（本大题共5个小题，每小题3分，共15分，将答案填在题中横线上）．
11．当x＝ 时，代数式
的值是0．
12．对于方程
，用含x的代数式表示y为
．
13．如果等腰三角形的顶角为80°，那么它的一个底角为 ．
14．已知－4＜x＜2，则x可取的负整数的和是 ．
15．AD为△ABC的高，AB＝AC，△ABC的周长为20cm，△ACD的周长为14cm，则AD＝ ．
三、解答题：（每小题6分，共30分）。
16．解方程 
17．解方程组 
18．解下列不等式组，并将它们解集在数轴 19．如图，已知在△ABC中，AB＝AC，∠ACD＝112°，
上表示出来：
求△ABC各内角的度数。
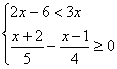
19．如图，已知∠BAC等于60°，点E、F分别位于 20．已知
是方程
∠BAC的两边上．试用刻度的直尺和量角器，在∠BAC 的解，求m 的值。
的内部寻找一点O，使点O到点E、F的距离相等，且
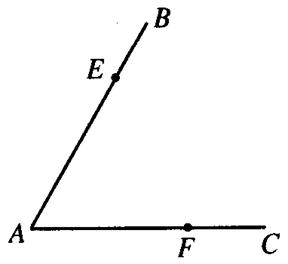到∠BAC的两边的距离相等．
四、解答题：（21、22题各6分，23题7分，24，25题各8分，共35分）．
21． 课外活动中一些学生分组参加活动，原来每组8人，后来重新编组，每组12人，这样比原来减少2组．
问这些学生共有多少人？
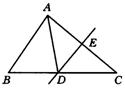
22．如图，在△ABC中，DE是AC的垂直平分线，AE＝3cm，△ABD的周长为13cm, 求△ABC的周长．
23．列不等式解下列应用题
某城市的出租汽车起步价为10元(即行驶距离在5千米以内都需付10元车费)，达到或超过5千米后，每行驶1千米加1.2元(不足1千米也按1千米计)．现某人乘车从甲地到乙地，支付车费17.2元，问从甲地到乙地的路程大约是多少?
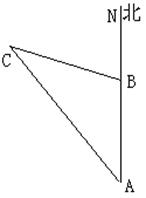
24． 如图所示，上午8时，一条船从A处出发，以15海里/时的速度向正北航行，10时到B处，从A，B望灯塔C，测得∠NAC＝42°，∠NBC＝84°，则从B处到灯塔C的距离是多少？
25．在社会实践活动中，某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量
(每小时通过观测点的汽车车辆数)，三位同学汇报高峰时段的车流量情况如下：
甲同学说：“二环路车流量为每小时10000辆”；
乙同学说：“四环路比三环路车流量每小时多2000辆”；
丙同学说：“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍”．
请你根据他们所提供的信息，求出高峰时段三环路、四环路的车流量各是多少?
(2003年，北京)