宜兴市升溪中学初一数学第二次阶段性测试卷
组卷：吉阿平 审核：初一年级数学备课组
一、耐心填一填（每小题2分，共24分）
1．当
时，代数式
与
的值相等．
2．由
可得到用x表示y的式子是 .
3．已知方程(a-2)xa-1+4=0 是关于x的一元一次方程，那么a= .
4．如果方程
是方程
的解，那么
5．一个三角形最多有a个锐角，b个直角，c个钝角，则a+b+c= .
6．掷二枚骰子，得到的点数和为4的成功率记为a，得的点数和为5的成功率记为b，则a与b的大小关系是
7．已知△ABC中，∠A＝
∠B＝
∠C，则△ABC是 三角形.
8．三角形的三个内角之比为3: 2:5，则该三角形最大的外角为 °.
9．某商品按原价的八折出售，售价为14.80元，那么原定价为 元.
10．等腰三角形两边长分别是5cm 和8cm，则其周长是 ..
11． 一个多边形的每一个外角都等于36°，那么这个多边形的内角和是 °
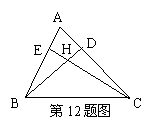
12．已知：如图，在△ABC中，∠A＝55°,H是高BD、CE的交点，则∠BHC＝ .
二、精心选一选（每小题只有一个正确答案，每小题3分，共21分）
11．下列方程中，是一元一次方程的是 （ ）
A、
B、
C、
D、
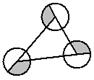12．如图，以三角形三个顶点为圆心画半径为2的圆，则阴影部分面积为（ ）
A、
B、2
C、3
D、4
13．下列说法不正确的是 （ ）
A、如果三角形有一个外角是锐角，那么这个三角形必为钝角三角形;
B、三角形的一个外角大于任何一个与它不相邻的内角.
C、含盐20%的盐水80克与含盐40%的盐水20克混合后就得到含盐30%的盐水100克;
D、方程
的正整数解只有2组.
16．四边形ABCD中，若∠A+∠C＝180°且∠B:∠C:∠D＝3:5:6，则∠A为 （ ）.
A.80°. B.70°. C. 60°. D.50°.
17．某人购买一种正多边形的瓷砖,铺设无缝地板,他购买的瓷砖形状不可以是 （ ）
A.正三角形. B.正四边形. C.正六边形. D.正八边形.
18．教科书117页游戏1中的“抢30”游戏，规则是：第一人先说“1”或“1、2”，第二个要接着往下说一个或二个数，然后又轮到第一个，再接着往下说一个或二个数，这样两个人反复轮流，每次每人说一个或两个数都可以，但不可以连说三个数，谁先抢到30，谁就获胜。若按同样的规则改为抢“40”，其结果是 （ ）
A、后报数者胜 B、先报数者胜 C、两者都可能胜 D、很难预料
19．一个三角形的两边长分别为5cm和3cm，第三边也是整数，且周长是偶数，则第三边长是A、 2cm或4cm B、 4cm或6cm C、4cm D、2cm或6cm （ ）
三、细心答一答（共55 分）
20．下列8个事件中：（本题4分）
（1）掷一枚硬币，正面朝上。 （2）打开电视机，正在播电视剧。
（3）随意翻开一本有400页的书，正好翻到第200页。 （4）天上下雨，马路潮湿。
（5）你能长到身高5米。 （6）买奖券中特等大奖。
（7）掷一枚骰子的得到的点数小于8。 （8）2006年6月8日是星期四。
其中（将序号填入题中的横线上即可）不可能事件为 ；必然事件为 ；不确定事件中，发生可能性最大的是 ，发生可能性最小的是
21. 观察以下图形，回答问题： （本题5分）
（1）图②有 个三角形；图③有___ _ 个三角形；图④有___ _个三角形；……
猜测第七个图形中共有 个三角形.
（2）按上面的方法继续下去，第
个图形中有 个三角形（用的代数式表示结论）.
22．解方程（组）或不等式（本题12分）
⑴解方程：
⑵解方程组
解下列不等式组，并把解集在数轴上表示出来.
⑶
⑷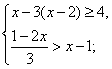 
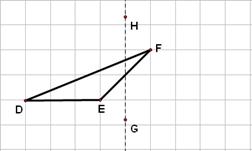
23. 如图，在正方形网格上有一个△ABC。（本题6分）
（1）作△DEF关于直线HG的轴对称图形（不写作法,保留痕迹.）;
（2）作EF边上的高（简述作法）;
（3）若网格上的最小正方形边长为1，求△DEF的面积.
 | |||
 | |||
|
25．在关于x、y的方程组
中，若
，求
的取值范围。
（本题5分）
27．如图，已知：在△ABC中，DE是BC的垂直平分线，DE交AC、BC分别于点D、E：
(1)当∠A=80，∠ABC=60时，求∠ABD的度数． （本题6分）
(2)当AB=10cm，AC=12cm时，求△ABD的周长．
28、如图，△ABC中，AB=AC，D为底边BC上任意一点，E为AC上一点，且AE=AD，。
（1）若∠BAD=30°∠B=65°，求∠EDC； （本题6分）
（2）给出一个关于∠BAD与∠CDE之间关系的猜想，并说明理由。
28．被誉为“竹的海洋”宜兴有着丰富的毛竹资源，某企业已收购毛竹52.5吨，根据市场信息，如果将毛竹直接销售，每吨可获利100元；如果对毛竹进行粗加工，每天可加工8吨，每吨可获利1000元；如果进行精加工，每天可加工0.5吨，每吨可获利5000元，由于受条件限制，在同一天中只能采用一种方式加工，并且必须在一个月（30天）内将这批毛竹全部销售，为此研究了两种方案： （本题7分）
方案一：将毛竹全部粗加工后销售，则可获利 元；
方案二：30天时间都进行精加工，未来得及加工的毛竹，在市场上直接销售，则可获利
元；
（1）试写出计算方案一、方案二所获利润的过程；
（2）是否存在第三种方案，将部分毛竹精加工，其余毛竹粗加工，并且恰好在30天内完成？若存在，求销售后所获利润；若不存在，请说明理由。