第9章 轴对称 单元测试卷
（满分：100分 时间：120分钟）
班级 姓名 成绩
一、选择题（每小题2分，共12分）
1．下列图形中，不是轴对称图形的是 （ ）
A．等边三角形 B．钝角三角形
C．线段 D．相交的两条直线
2．在等腰三角形中，两个内角的比为
，则顶角为
（ ）
A．
B．
C．或
D．或
3．在△
的内部有一点
，点与
关于
对称，点与
关于
对称，则△
是
（ ）
A．等边三角形 B．等腰三角形
C．直角三角形
D．钝角三角形
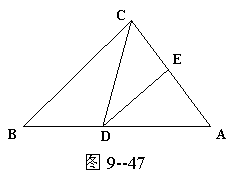
4．图9-47中，
是
的垂直平分线，
厘米.
厘米， 则△
的周长为 ( )
A．
厘米
B．
厘米
C．
厘米
D．
厘米
5．等腰三角形顶角的外角平分线与底边关系是 （ ）
A．平行均数 B．垂直
C．相交 D．无法确定
6．到三角形三边的距离相等的点是 （ ）
A．三边的垂直平分线的交点 B．三边中线的交点
C．三个角的平分线的交点 D．三条边上的高的交点
二、填空题（2、4、6每小题4分，其它每小题3分，共33分）
1．按要求填写一个符合条件的图形名称：
(1)一条对称轴：____________；(2)两条对称轴：____________；
(3)三条对称轴：____________；(4)四条对称轴：____________；
(5)五条对称轴：____________；(6)无数条对称轴：____________.
2．在一个等腰△
，
(1)若
，则
是_________角，其值为______________；
(2)若
，则顶角是___________________；
(3)若其中两边是
厘米和
厘米，则△的周长是___________________；
(4)若其中两边是
厘米和厘米，则△的周长是___________________.
3．在等腰△中，
，
是边上的高，且
，则顶角
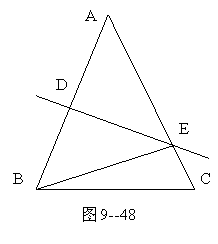
4．如9-48在△中，
厘米，垂 直平分
，（1)若
厘米，则△
的周长是__________厘米；(2)若
，则
5．在一张纸上写着一个数，在镜子中成如图9-49所示的形状，则纸上写的数为___________.
6．如图9-50一条船从
处出发，以
里/小时的速度向正北方向航行，
个小时到达
处，从、望灯塔，得
，
，则到灯塔
的距离是______________.
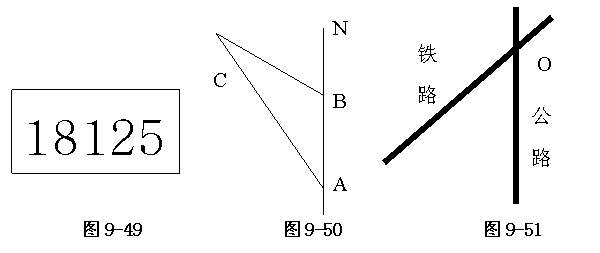
7．某学校到公路距离与到铁路的距离是相等的，并且到公路和铁路相交处
点的距离是
千米.在图9-51中标出学校的位置，理由是____________________________.
8．在△中，的垂直平分线交
于
，交于
，△
的周长是厘米，
厘米，△的周长是_______________________.
9．把一张纸对折次后，用针扎一个孔，将其展开，这张纸上共有____________个小孔．
10．一个正整数
，如果把它的各位数字颠倒过来所得的数仍是，则称为回文数，如
，
，
等．从对称的角度看，回文数亦可以看做是轴对称的数．年份数
也是一个回文数，从
至
年这
年年份中，回文数一共有___________个.
三、解答题（每小题分值见题目，共55分）
1．作图:(1)在直线
上求作一点，使
最小．（本小题8分）
(2)在直线l上求作一点，使
最大．（本小题8分）
2．利用轴对称知识画图：
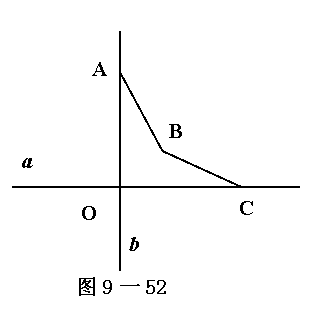
(1)作出如图9-52中图形
关于直线
、
对称的图形；（本小题4分）
(2）由（1）得到的星形图形中有_______________条对称轴；（本小题4分）
(3)用剪刀剪出这个星形图，正方形纸片需要沿对角线折__ ____次．（本小题6分）
3．一个△，
，过点的直线将这个三角形分成
个等腰三角形，试确定
的度数. （本小题10分）
4．（1）如图9-53所示，在长方形
的对称轴上找点，使△
、△
、△
和△
都是等腰三角形. （本小题8分）
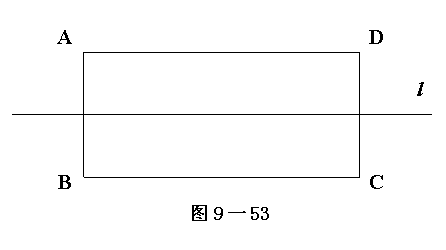
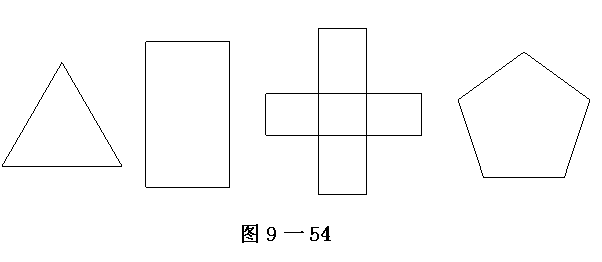
（2）画出图9-54中图形的所有对称轴．（本小题7分）
答案
一、1．B 2．D 3．B 4．A 5．A 6．C
二、1．（1）等腰三角形 （2）长方形
（3）等边三角形 （4）正方形
（5）正五边形 （6）圆
2．（1）底，
（2）
或
（3）
cm
（4）
㎝或
cm
3．或
4．（1） （4）
5．
或
6．
里
7．在角平分线上且
㎜ 8．cm
9．
10．
三、1．（1）作关于的对称点
，连结
，线段与交于，
则就是所求点.也可作关于的对称点
（2）作关于的对称点，直线与交于，则就是所求点. 也可作关于的对称点
2．（1）略
（2）条 （3）次
3．如图，分成两类进行研究：
（1）为
的底角，如果
，那么
；如果
为
的底角，那么
或；如果为的顶角，那么
；如果
，那么
，所以
（2）为的顶角，这时，
，所以
，综上所述，的值为或
或
或
4．当垂直平分时，因为在对称轴上，所以
与
必定是等腰三角形，
与
关于对称，因此只要研究即可，在中再分三种情况：为顶角时，以为圆心，
为半径作圆弧与交于点；为顶角时，以为圆心，为半径作圆弧交于点，为顶角时，作的垂直平分线与交于点．当垂直平分时，作类似的研究．若该长方形的邻边不相等时，共有个点符合条件．若该长方形为正方形时，只有一个点符合条件，这就是其中心。