中山市2005学年度下学期期末水平测试试卷
七年级数学
| 题号 | 一 | 二 | 三 | 总 分 | |||||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||||||||
一、单项选择题：（3分×5=15分，请将唯一正确答案的字母填入题后的括号内）
1、x = 3是方程x + a = 4的解，则a的值为 （ ）
A．7 B．1 C．－1 D． －7
2、下列正多边形中，不能够铺满地面的是 （ ）
A．正三角形 B． 正方形 C．正五边形 D．正六边形
3、下列图形中，只有一条对称轴的轴对称图形是 （ ）
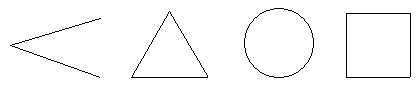
A．角 B．等边三角形 C．圆 D．正方形
4、下列调查中，不适合作抽样调查，而应作普查的是 （ ）
A．调查市场上冰淇淋的质量
B．审查七年级（下）数学教材有无科学性错误
C．调查市场上各种品牌电视机的使用寿命
D．调查全世界爱滋病发病情况
5、布袋里有1个红球、2个白球，从中同时摸出2个球，下列事件中必然事件是（ ）
A．摸出2个白球 B．摸出1个红球，1个白球
C．摸出2个红球 D．至少摸出1个白球
二、填空题（3分×5=15分）
6、n边形的内角和是
7、“抛掷两枚硬币”的游戏中，出现两个正面的机会约为
8、等腰三角形有一内角为
，则另外两个内角分别为_____________、____________
9、x = 5是方程 x－3 = a的解，则a =
10、为估计池塘里鱼的条数，先从池塘里捕捞一网，共捕到20条鱼，将它们全部标上记号后放回池塘，当它们完全混合于鱼群中后，又捕捞了三网，共捕到54条鱼，其中有3条鱼标有记号，据此可估计池塘里大约有 条鱼。
三、解答题（共70分，要写出解题过程）
11、（5分）解方程：3 (x－2)＋1= x － (2x－1)
12、（5分）解方程组：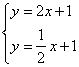
13、（5分）n边形的内角和为1980
，求边数n.
14、（5分）x为何值时，代数式4 x － 5的值比3 x — 6的值小1？
15、（5分）如图，△ABC与△A1B1C1是轴对称图形，请画出它们的对称轴（保留作图痕迹）.
 |
16、（6分）在方格纸内分别画一个轴对称的三角形和四边形，要求三角形和四边形的顶点都在小正方形的顶点上。
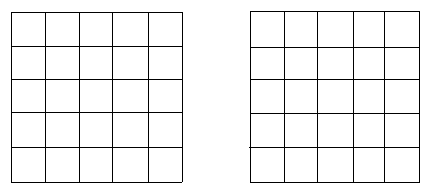
①三角形 ②四边形
17、（6分）如图，△ABC中，
求
、
的度数。
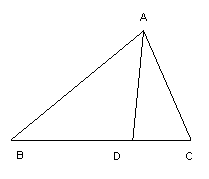
18、（6分）如图，ΔABC是等边三角形，BD是∠ABC的平分线，延长BC到E，使CE=CD，连接DE。请指出图中有哪些相等的线段？有哪些角等于30°？
 |
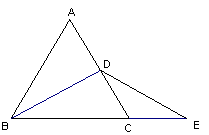19、（6分）小王用36元钱购买邮票，一共购得0.8元面值与2元面值的邮票30张，问小王购买0.8元面值与2元面值的邮票各多少张？
20、（6分）若方程组
的解也是方程组
的解，求a、b之值.
21、（7分）某工厂职工的月工资及人数如下表：
| 月工资数（元） | 人 数 |
| 10 000 | 1（总经理） |
| 8 000 | 2（副总经理） |
| 5 000 | 2（经理） |
| 2 000 | 5 |
| 1 000 | 12 |
| 900 | 18 |
| 800 | 23 |
| 700 | 5 |
| 500 | 2 |
（1）求职工月工资的众数、中位数与平均数；
（2）用哪一个数作为月工资的代表数比较合理，说明你的理由.
22、（8分）如图，P为
内任意一点，点P关于OA、OB的对称点分别为
、
，
（1）说明ΔO为等腰三角形；
（2）探究满足什么条件时，ΔO为等边三角形，说明你的理由。
中山市2004–2005学年度下学期期末水平测试试卷
七年级数学参考答案与评分建议
一、B、C、A、B、D．
二、6．(n-2)180°； 7．
； 8．45
，45； 9． 2 ； 10．360 ；
三、11．
； 12．
； 13．n =13； 14．x =－2
15．（略） 16．（略） 17．
40，
70
18．相等的线段有：BD=DE，AD=CD=CE，AB=AC=BC（3分）；
ABD =DBC =EDC =DEC =30（3分）。
19．设小王购买0.8元面值与2元面值的邮票分别为x、y张（1分）
则 
（3分） 解之得 
（5分）
答：小王购买0.8元面值邮票20张，2元面值的邮票10张。（6分）
20．解方程 得 
（2分），
代入 可得：
（4分）
解之得：a = 
，b = — 
（6分）
21．（1）众数= 800 （1分） 中位数 = 900 （2分） 平均数 ≈1387.14 （2分）
（2）用众数或中位数作代表数比较合理，众数代表了大多数人的工资水平，中位数代表了工资的中间水平。（2分）
22．（1）连结OP，因为O= OP = O，所以O= O，
ΔO为等腰三角形（4分）
（2）因为OA =AOP，BOP =OB，
所以 O= 2AOB，
当O= 60 ，即AOB = 30时，ΔO为等边三角形。