2004—2005学年度第二学期
七年级数学第八章测试题
班别________姓名____________座号______得分___________
一、选择题。(每小题3分,共30分)
1、下列给出的方程中是二元一次方程的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、当k=( )时,方程![]() 是二元一次方程。
是二元一次方程。
A、1 B、-1 C、3 D、-3
3、已知y=ax+b,当x=1时,y=-1;当x=3时,y=5。则有( )
A、a=3,b=-4. B、a=-3,b=4. C、a=4,b=-3. D、a=-4,b=3.
4、已知![]()
![]() 则( )。
则( )。
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、对于方程组(I)![]() 和方程(II)7x+3y=12.下列说法正确的是:( ).
和方程(II)7x+3y=12.下列说法正确的是:( ).
A、 I的解必是II的解 B、II的解必是I的解
C、I的解不是II的解 D、II的解不是I的解
6、若方程![]() 的解x与y的和为0。则k的值为:( )
的解x与y的和为0。则k的值为:( )
A、k=-2 B、k=0 C、k=4 D、k=2
7、用加减法解方程组![]() 时,下列的变形式中,正确的是:( ).
时,下列的变形式中,正确的是:( ).
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
|
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、在方程2(x +y)-3(y—x)=3中,用含x式子表示y,则( ).
A、y=5x—3 B、y=-x—3 C 、![]() D、y=3-5x
D、y=3-5x
10、在等式y=kx+b中,当x=0,y=1;当x= -1,y=3.则这个等式为:( ).
A、y=2x+1 B、y=-2x+1 C、y=-2x-1 D、y=2x-1
二、填空题。(每小题3分,共30分)
1、 在二元一次方程2x+3y=a中,当x=2,y=-1时,a=___________.
2、 方程2x-y=3与3x+2y=1的公共解是______________.
3、 在方程4x-2y=13中,当x=-3时,y=_____________.
4、 若![]() 与
与![]() 都是方程y=kx+b的解,则k=________,b=_______.
都是方程y=kx+b的解,则k=________,b=_______.
5、 解方程组![]() 若用代入法解最好将方程_____变形,用含_____
若用代入法解最好将方程_____变形,用含_____
的代数式表示_______得________________,再代入方程_________.
6、 已知![]() 是二元一次方程,则m=_______,n=________.
是二元一次方程,则m=_______,n=________.
7、 二元一次方程3x+2y=12的所有非负整数解为_______________________.
8、 若![]() 与
与![]() 是同类项,则
是同类项,则![]() __________.
__________.
|
9、 当m=________时,方程组 无解。
10、设“■”“●”表示两面种不同的物体,现用天平称两次,如下图所示,那么
这两种物体的质量分别为■=_________,●=__________.
![]()
|
![]()
![]() ■●●
■ ● 10g
■●●
■ ● 10g
|
三、解答题。(共40分)
1、解下列方程组。(每小题5分)
⑴用代入法解![]() ⑵用加减法解
⑵用加减法解![]()
⑶![]() ⑷
⑷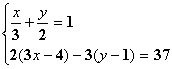
|
3、运往某地一批化肥,第一批600吨,需用9节火车皮和12辆汽车;第二批430吨,需用6节火车皮和14辆汽车。若用4节火车皮和6辆汽车可以运走多少吨化肥?(6分)
4、某中学新建一栋4层的教学大楼,每层楼有8间教室,进出这栋楼共有4道门,其
中两道正门大小相同,两道侧门大小也相同。安全检查中,对4道门进行了测试:当
开启一道正门和两道侧门时 ,2分钟内可以通过560名学生;当同时开启一道正门
和一道侧门时, 4分钟内可以通过800名学生。
(1) 求平均每分钟一道正门和一道侧门各可以通过多少学生?
(2) 检查中发现,紧急情况时因学生拥挤,出门的效率将降低20%,安全检查规定,在
紧急情况下全大楼的学生应在5分钟内通过这4道门安全撤离,假设这栋大楼每间教室最多有45名学生,问:建造的这4道门是否符合安全规定?请说明理由。(8分)
|
答案
一、选择题。BDADA DCCAB
二、(1)1(2)x=1,y=-1(3)-12![]() (4)1,0(5)②,x,y,y=5x-3,①(6)4,-
(4)1,0(5)②,x,y,y=5x-3,①(6)4,-![]() (7)x=0 y=6;x=2 y=3;x=4 y=0(8)3(9)4(10)30g,20g
(7)x=0 y=6;x=2 y=3;x=4 y=0(8)3(9)4(10)30g,20g
三、解答题,
1、(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]()
2、解:设甲工程队有X人。乙工程队有Y人。
![]()
解这个方程组得:![]()
3、解:设每节火车皮可以运走X吨,每辆汽车可以运走Y吨。
![]()
解这个方程组得:![]()
4、(1)解:设平均每分钟一道正门可以通过X人,一道侧门可以通过Y人。
![]()
解这个方程组得: ![]()
(2)这楼最多有学生4×8×45=1440(名)
拥挤时5分钟4道门可以通过:5×2(120+80)(1-20%)=1600(名)
1600>1440。所以可以全部安全撤离。