![]()
![]()
![]()
 2005-2006学年第二学期期中
2005-2006学年第二学期期中
初一年级数学质量检测试题
|
一、选择题: (每题3分,共30分)
1.![]() 的计算结果是( ).
的计算结果是( ).
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.下列说法正确的是( ).
(A)对顶角相等 (B)同位角相等
(C)内错角相等 (D)同旁内角相等
3.2005年10月17日,“神六”航天员费俊龙、聂海胜经过115个小时32分的太空飞行,走出返回舱.这次航天员的太空之旅为325万千米,这个数用科学记数法表示是( )米.
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)![]()
 4.如图1,在这三张扑克牌中任意抽取一张,
4.如图1,在这三张扑克牌中任意抽取一张,
抽到“红桃7”的概率是( ).
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D) ![]() 图1
图1
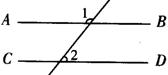 5.如图2,
5.如图2,![]() ,则
,则![]() 等于( ).
等于( ).
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D)![]()
图2
6.下例运算中,运用完全平方公式计算正确的是( ).
(A)![]() (B)
(B) ![]()
(C)![]() (D)
(D) ![]()
7.下列多项式乘法中,可以用平方差公式计算的是( ).
(A)![]() (B)
(B) ![]()
(C)![]() (D)
(D) ![]()
8.如图3,下列说法中正确的是 ( ).
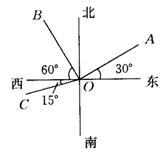 (A)
(A)![]() 的方向是北偏东
的方向是北偏东![]()
(B) ![]() 的方向是北偏西
的方向是北偏西![]()
(C) ![]() 的方向是北偏西
的方向是北偏西![]()
(D) ![]() 的方向是南偏西
的方向是南偏西![]() 图3
图3
9.三个连续偶数,中间的一个是![]() ,
,
则这三个偶数的和是 ( ).
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.多项式![]() 是( ).
是( ).
(A)一次多项式 (B)二次多项式 (C)三次多项式 (D)四次多项式
二.填空: (每题3分,共15分)
 11.
11.![]() 的系数是________.
的系数是________.
12.计算:![]() =________.
图4
=________.
图4
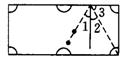
13.在图4的长方形台球桌面上,如果![]() ,则
,则![]() .
.
14.已知,![]() ,那么
,那么![]() 的补角等于________度.
的补角等于________度.
15.如果![]() ,那么
,那么![]() .
.
三.解答题: (本部分共7题,其中第16、17、18题各10分,第19、20、21题各6分,第22题7分,共55分)
16.计算:
(1)![]() ; (2)
; (2)
![]()
17.化简求值:
(1)![]() ,其中
,其中![]()
(2)![]() ,其中
,其中![]()
18. 如图5,求阴影部分的面积.
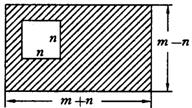
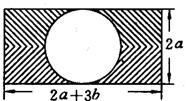
(1) 图5 (2)
19.如图6,一束平行光线![]() 与
与![]() 射向一个水平镜面后反射,
射向一个水平镜面后反射,
此时,![]() ,
,![]()
①![]() 的大小有什么关系?为什么?
的大小有什么关系?为什么?![]() 与
与![]() 呢?
呢?
②反射光线![]() 与
与![]() 也平行吗?为什么?
也平行吗?为什么?
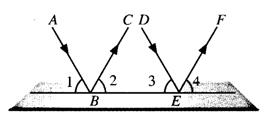
图6
20.一张写有密码的纸片被随意地埋在如图7所示的矩形区域内
(共4个方格,每个方格大小都是一样的)
(1)请猜想埋在哪个区域的可能性大?
(2)分别计算埋在三个区域内的概率。
(3)埋在那两个区域的概率相同?
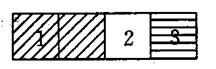
图7
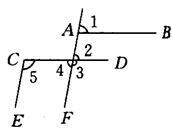 21.如图8,
21.如图8,![]() ,
,![]() ,
,![]() ,
,
![]() 与
与![]() 平行吗?为什么?
平行吗?为什么?
图8
22.如图9,![]() 与
与![]() 互补,
互补,![]() ,探求
,探求![]() 与
与![]() 的位置关系.
的位置关系.
解:∵ ![]() (
)
(
)
![]() 与
与![]() 互补,( )
互补,( )
∴![]() 与
与![]() 互补,(等量代换)
互补,(等量代换)
∴![]() (
)
(
)
∴![]() (
)
(
)
又∵![]() (
)
(
)
∴![]() (
)
(
)
∴![]() (
)
(
)
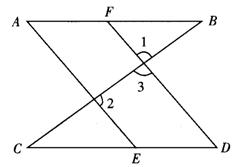
图9