一元一次不等式（组）
一、填空题
1．已知不等式3x-a≤0的正整数解恰是1，2，3，则a的取值范围是 。
2．已知关于x的不等式组
无解，则a的取值范围是
。
3．不等式组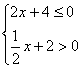
的整数解为
。
4．如果关于x的不等式（a-1）x<a+5和2x<4的解集相同，则a的值为 。
5．已知关于x的不等式组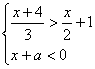
的解集为
，那么a的取值范围是 。
二、选择题
6．不等式组
的最小整数解是（
）
A．0 B．1 C．2 D．-1
7．若-1<a<b<0，则下列式子中正确的是（ ）
A．-a<b B．
C．
D．
8．若方程组
的解满足条件
，则k的取值范围是（ ）
A．
B．
C．
D．
9．如果关于x的不等式组
的整数解仅为1，2，3，那么适合这个不等式组的整数对（m，n）共有（ ）
A．49对 B．42对 C．36对 D．13对
10．关于x的不等式组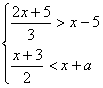
只有5个整数解，则a的取值范围是（ ）
A．
B．
C．
D．
三、解答题
12．
13．已知a、b、c是三个非负数，并且满足3a+2b+c=5，2a+b-3c=1，设m =3a+b-7c，记x为m的最大值，y为m的最小值，求xy的值。
14．已知关于x、y的方程组
的解满足
，化简
。
15．已知
，求
的最大值和最小值。
16．某饮料厂为了开发新产品，用A、B两种果汁原料各19千克、17.2千克，试制甲、乙两种新型饮料共50千克，下表是试验的相关数据：
|
| 甲 | 乙 |
| A（单位：千克） | 0.5 | 0.2 |
| A（单位：千克） | 0.3 | 0.4 |
（1） 假设甲种饮料需配制x千克，请你写出满足题意的不等式组，并求出其解集。
（2） 设甲种饮料每千克成本为4元，乙种饮料每千克成本为3元，这两种饮料的成本总额为y元，请写出y与x的函数表达式，并根据（1）的运算结果，确定当甲种饮料配制多少千克时，甲、乙两种饮料的成本总额最少？
17．据电力部门统计，每天8点至21点是用电高峰期，简称“峰时”，21点至次日8点是用电低谷期，简称“谷时”。为了缓解供电需求紧张的矛盾，我市电力部门拟逐步统一换装“峰谷分时”电表，对用电实行“峰谷分时电价”新政策，具体见下表：
| 时间 | 换表前 | 换表后 | |
| 峰时（8点至21点） | 谷时（21点~次日8点） | ||
| 电价 | 0.52元/千瓦时 | x元/千瓦时 | y元/千瓦时 |
已知每千瓦时峰时价比谷时价高0.25元，小卫家对换表后最初使用的100千瓦时用电情况进行统计分析知：峰时用电量占80%，谷时用电量点20%，与换表前相比，电费共下降2元。
（1） 请你求出表格中的x和y的值；
（2） 小卫希望通过调整用电时间，使她家以后每使用100千瓦时的电费与换表前相比下降10元至15元（包括10元和15元）。假设小卫家今后“峰时”用电量占整个家庭用电量的z%，那么：在什么范围时，才能达到小卫的期望？
答案提示：
1，9＜a≤12 2,a＞3 3，-2;-3 4，7 5，a≤-2
6，A 7 ，D 8，A 9，B 10，C
12，x≥8
13，
14，3或者2a-3
15，最大值是4，最小值为
16，28≤x≤30 y=150+x,当x=28时，y最小为178
17，x=0.55 y=0.3 28≤z≤48