七年级（上）数学试题
一、1、下面几组数中，不相等的是 ( )
A、 －3和+(－3) B、 －5和－(+5)
C、－7和－(－7) D、+2和│－2│
2、平面上有任意三点，过其中两点画直线，共可以画（ ）
A、1条 B、3条 C、1条或3条 D、无数条
3、在数轴上表示a、b两数的点如图所示，则下列判断正确的是（ ）
A、a+b＞0 B、a＋b＜0 C、ab＞0 D、│a│＞│b│
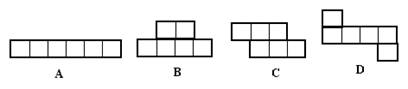
4、下列图形中，哪一个是正方体的展开图（ ）
5、2002年11月23—29日在泉州销售8000万元即开型福利彩票（每张面额2元），特等奖100万元，结果中一百万元者有15名，假如你花10元买5张，下列说法正确的是写 （ ）
A、中一百万元是必然事件 B、中一百万元是不可能事件
C、中一百万元是可能事件，但可能性很小
D、因为5÷15＝1/3，所以中一百万元的可能性是33.3％
6、计算（－1）1001÷(－1)2002所得的结果是（ ）
A、1/2 B、－1/2 C、1 D、－1
7、任何一个有理数的平方（ ）
A、一定是正数 B、一定不是负数 C、一定大于它本身 D、一定不大于它的绝对值
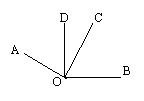8、如图，
和
都是直角，如果
，那么
（ ）
A、
B、
C、
D、
二、9、计算：０－1＝___________。
10、据2003年12月29日，中央气象台预报，下列四个地区的最低气温分别是：哈尔滨－10℃，杭州5℃，兰州－6℃，南沙26℃，请你把这四个气温按从高到低的顺序排列：_____________________。
11、人体中的红细胞个数约有25,000,000,000,000，用科学记数法表示这个数为：_____________ 。
| 同学 | 甲 | 乙 | 丙 | 丁 |
| 身高 |
| 3 | 0 | -5 |
12、俯视图为圆的立体图形可能是______________________。
13、某中学的校运动会需要为开幕式选拔仪仗队队员，规定每位同学的身高是165厘米，测量了4个同学的身高，超过规定身高的厘米数记作正数，不足规定身高的厘米数记作负数，检查四个同学的结果如右：哪一个同学的身高符合仪仗队队员的标准？为什么？_____________________。
14、对单项式“5x”，我们可以这样来解释：某人以５千米／小时的速度走了x小时，他一共走的路程是5x千米，请你对“5x”再给出另一个生活实际方面的解释： ___________________________________________________________。
15、把多项式：x2－1＋2x－3x3按x降幂排列：_________________________________。
16、下午２点整时，时针与分针所组成的角为_________度
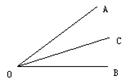
17、如图， OC平分∠AOB，∠BOC＝20°，则∠AOB＝_______。
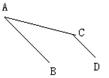
18、如图，如果AB∥CD，那么∠A与∠C_______。
19、请你写出两个有理数，并把它们相加，使它们的和小于每一个加数___________。
20、小凡在计算时发现，11×11=121，111×111=12321，1111×1111=，他从中发现了一个规律。你能根据他所发现的规律很快地写出 ×= ?
答案是___________________________。
三、21、计算：3×(－4)＋(－28) ÷7 22、计算：4×(－3)2－15÷(－3)－50
23、求代数式 (2a2－5a)－2(3a＋5－2a2)的值，其中a＝－１
四、24、南安位于福建东南沿海，历史悠久，人杰地灵，全市总面积2036平方千米，截止2001年12月，全市人口达人。
１、把全市人口数取近似值（精确到万位）≈____________，
２、全市面积2036平方千米≈__________________________平方米（保留3个有效数字）
３、计算全市人均占有土地面积（精确到１平方米）≈________m2≈________亩（保留1位小数）
五、参观图形大观园
25、（8分）如图，已知C点为线段AB的中点，D点为BC的中点，AB＝10cm，求AD的长度
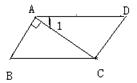26、（12分）如图，已知∠1＝30°，∠B＝60°，AB⊥AC
（1）计算：∠DAB＋∠B
（2）AB与CD平行吗？AD与BC平行吗？
27、（8分）定义一种新运算：﹡，观察下列式子：
1﹡3 = 1×3＋3 = 6 3﹡2 = 3×2＋2 = 8
3﹡5 = 3×5＋5 = 20 5﹡3 = 5×3＋3 =18
（1）请你仿照上述运算方法，计算：
﹡7的值。（写出过程）
（2）请你猜想 
﹡
=
；﹡=
；
（3）若
，则﹡
﹡（填“=”或“
” ）
（4）试计算：2﹡
（写出过程）
六、学以致用
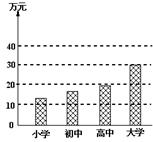28、（10分）国家统计局最近公布的《首次中国城市居民家庭财产调查总报告》显示，截止2002年6月底，我国城市居民家庭财产总值户均达22.83万元。其中户主文化程度为小学、初中、高中、大学毕业的户均财产数值如上图所示：
1、户均财产最多的户主的文化程度是__________________________，
2、户均财产最少的户主的文化程度是__________________________，
3、从图中可发现：文化程度越高，家庭财产____________________，
4、在平均线22.83万元以下的文化程度是__________________________。
29、（12分）某市的出租车因车型不同，收费标准也不同：A型车的起步价10元，3千米后每千米价为1.2元；B型车的起步价8元，3千米后每千米价为1.4元。
（1）如果你要乘坐出租车到20千米处的地方，从节省费用的角度，你应该乘坐哪种型号的出租车？
（2）请你计算乘坐A型与B型出租车x（x＞3）千米的价差是多少元？
30、邮购一种图书，每本定价
元，不足100本时，另加书价的5％的邮资．
（1）要邮购
的正整数）本总计金额是多少元？
（2）当一次邮购超过100本时，书店除付邮资外，还给予优惠10％．
计算
元，
本时的总计金额是多少元？
六、作图，并回答（1）以A为顶点，在三角形外作∠BAE＝∠ABC
（2）在AE上裁取AM＝BC
|
并观察上图，线段BM与AC有何关系
|
|
2、解决下列问题：
①用一根长 80厘米的绳子围成一个长方形，且这个长方形的长比宽多10厘米，则这个
长方形的长和宽各是多少7这个长方形的面积是多少？
②用这根绳于围成一个正方形，则这个正方形的边长是多少？面积是多少？
③如果用这根绳于围成一个圆，则这个圆的半径是多少，面积是多少？（可取3.14）
④再分别取长度 100厘米，120厘米的绳子重复上面的①②③运算比较得出的结果.
你能获得什么猜想。
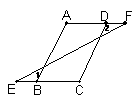3、如图，已知：∠1=∠2，∠A=∠C，说明∠E=∠F的理由
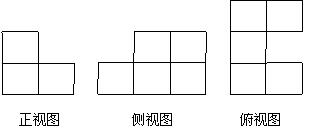4、一个物体由若干个大小一样，边长为1的正方体木块垒成，它的三视图如下，请回答：
（1）该物体有多少层高？
（2）该物体由多少块木块垒成？
初一年数学期末测查参考试卷(一)参考答案：
一、（每题4分）1、C，2、C，3、B，4、D，5、C，6、D，7、B，8、A
二、（每题3分）9、－1，10、26℃＞5℃＞－6℃＞－10℃，11、2.5×1013，12、球体、圆柱、圆锥，13、丙，14、略15、－3x3＋x2＋2x－1，16、60°，17、40°，18、互补，19、略，20、4321
三、21、原式=－12＋（－4） =－16
22、原式=4×9－（－5）－50 =36＋5－50=－9
23、原式= 2a2－5a－(6a＋10－4a2) = 2a2－5a－6a－10＋4a2= 6 a2－11a－10
当a=－1时，
原式= 6×（－1）2－11×（－1）－10= 6＋11－10= 7
四、24，1、147万，2、2.04×109，3、1380，2.0
五、25、点C是线段AB的中点
AC= CB = 1/2AB = 5cm
点D是线段CB的中点
CD = DB = 1/2 CB =2.5 cm
AD = AC＋CD = 7.5 cm
26、（1）AB⊥AC
∠CAB = 90°
∠DAB＋∠B = ∠1＋∠CAB＋∠B= 30°＋ 90°＋ 60°= 180°
（2）AB与DC平行，
因为内错角相等，两直线平行；
AD与BC平行，
因为同旁内角互补，两直线平行。
27、略
六、28、（1）大学（2）小学（3）越多（4）小学、初中、高中
29、（1）乘坐A型出租车费用
= 10 ＋（20－3）×1.2= 10 ＋20.4
= 30.4 （元）
乘坐B型出租车费用
= 8 ＋（20－3）×1.4= 8 ＋23.8= 31.8 （元）
因为30.4＜31.8所以乘坐A型出租车费用较少。
（2）乘坐A型出租车x（x＞3）千米费用
= 10 ＋（x－3）×1.2= 1.2x＋6.4
乘坐B型出租车x（x＞3）千米费用
= 8 ＋（x－3）×1.4 = 1.4x＋3.8（元）
乘坐A、B型出租车x（x＞3）千米的价差
= （1.2x＋6.4）－（1.4x＋3.8）= －0.2x＋2.6（元）
或0.2x－2.6（元）