成都七中实验学校2005～2006学年度下期期末素质测试
七 年 级 数 学
（命题人： 刘建泽）
| 题号 | A 卷 | A卷 总分 | A 卷 | B卷 总分 | 全卷 总分 | |||||||
| 一 | 二 | 三 | 四 | 五 | 一 | 二 | 三 | 四 | ||||
| 得分 |
|
|
|
|
|
|
|
|
|
|
|
|
本试卷分为A卷和B卷,A卷满分100,B卷满分50分,全卷总分150分.考试时间120分钟
A 卷（100分）
一、 选择题(每小题3分，共30分.) 下列各小题只有一个正确答案，请把你认为正确的答案填在下表中。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1．下列计算正确的是：
（A）
（B）
（C）
（D）
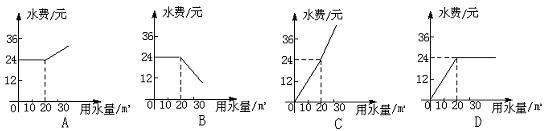
2．某市为了节约用水，按以下规定收取水费：(1)每户每月用水量不超过20 m3，则每立方米水费1.2元；(2)每户每月用水量超过20 m3，则超过的部分每立方米水费2元，下面可以刻画出该户交纳水费随用水量的变化情况大致图象为：
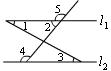
3．如图，下列条件中，不能判断直线l1∥l2的是：
A、∠1=∠3 B、∠2=∠3
C、∠4=∠5 D、∠2+∠4=180°
4．已知a，b，c是△ABC的三边， a＝2，b＝5且三角形的周长是偶数，则c等于：
A．4 B．6 C．5 D．4或6
5．一个囗袋里有5个白球、3个红球，从中任摸两球，则摸到两个都是红球的概率是：
A、
B、
C、
D、
6.下列图形中，轴对称图形的个数有：
A．4个 B．3个 C．2个 D．1个
7．如图(1),小明拿一张正方形纸片，沿虚线对折一次得到图(2),再对折一次得到图(3),然后用剪刀沿图(3)中的虚线剪去一个角再打开后的形状是：
|
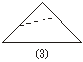
实际时间是 ：
A．21：10 B. 10：21 C. 10：51 D. 12：01
9．珠穆朗玛峰是世界第一高峰，它的海拔高度约为8848米.它高度的百万分之一相当于:
A、 3层楼的高度 B、大象的高度. C、 袋鼠的高度 D、两个作业本的厚度
10．某种原子的半径为2纳米，相当于（ ）米。
A、0.2×10-10 B、2×10-10 C、2×10-11 D、0.2×10-11
| |
 |
11．单项式 的系数是_________, 次数是__________.
12．计算 
＝___________
13．近似数12.30万精确到 位，有______个有效数字.
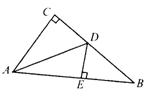14．如图，△ABC中，AD平分∠BAC，∠C＝90°，
DE⊥AB交AB于E，BC＝12，BD＝2CD，
则DE的长是___________．
15．一个角的余角与它的补角之比为1：5，
则这个角的大小是
三、解答下列各题（每小题7分，共21分）
16、(－x－2y)(x2－4y2)(x－2y)
17. 已知x－y＋4＝0，求
的值
18．如图，AB∥CD，FG∥HD，∠B=100º，FE为∠CEB的平分线，求∠D的度数.
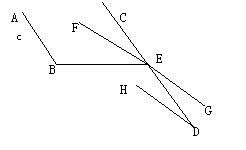
四、（每小题8分，共16分）
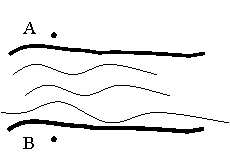
19．如图，要测量河两岸A,B两点间的距离，测量工具只有卷尺和量角器，
请设计一个能求河宽AB的方案，并说明理由。
20．如图，在一条河的同岸有两个村庄A、B，两村要在河上合修一座桥到对岸去，桥修在什么地方，可以使两个村庄到桥的距离之和最短？请作出这个点，并说明理由。
五、（每小题9分，共18分）
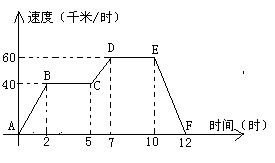21．根据图像回答下列问题：
（1）该图反映的两个变量中，自变量是
___________, 因变量是___________.
（2）线段BC，点D和点F分别代表了什么？
（3）说一说速度是怎样随时间的变化而变化的；
（4）想象一个大致符合图中所刻画的关系的实际情景，并把它描述出来。
22． 2001年7月13日晚上21点55分，国际奥委会主席萨马兰奇郑重宣布：“2008年夏季奥运会主办城市是——北京。” 以下是一体育爱好者收集的有关奥运会的部分资料：
表一：中国奥运奖牌回眸
| 届数 | 金牌 | 银牌 | 铜牌 | 合计 |
| 第23届 | 15 | 8 | 9 | 32 |
| 第24届 | 5 | 11 | 12 | 28 |
| 第25届 | 16 | 22 | 16 | 54 |
| 第26届 | 16 | 22 | 12 | 50 |
| 第27届 | 28 | 16 | 15 | 59 |
表二：第27届奥运会奖牌总数前五名统计表
| 代表队 | 金牌 | 银牌 | 铜牌 | 合计 |
| 美国 | 39 | 25 | 33 | 97 |
| 俄罗斯 | 32 | 28 | 28 | 88 |
| 中国 | 28 | 16 | 15 | 59 |
| 澳大利亚 | 16 | 25 | 17 | 58 |
| 德国 | 14 | 17 | 26 | 57 |
| 其他 | 172 | / | / | / |
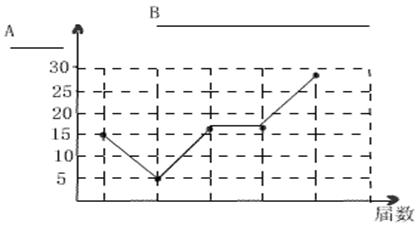
⑴下图是小明根据表格数据所制作的折线图. 请你帮小明给这张统计图在A处加上名称、在B处加上标题，同时还有表示不太清楚的地方请你把图形表示更太清楚一些。
⑵你可从中获得哪些信息？写出3条。
⑶小明还想制作一张统计图，用来形象地比一比：中国、美国、俄罗斯、澳大利亚、德国，那一国在第27届奥运会上金牌多，你认为他应该制作什么统计图比较合理？请帮小明画出这张图。
B 卷 (50分)
一、 填空题（每小题4分，共20分）
23．现规定一种运算：a★b＝ab＋b－a,则(b－a)★b＝__________________.
24．用边长60cm的正方形铁皮做一个无盖水箱,先在四个角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成,如果截去的小正方形的边长是xcm,水箱的容积是ycm3,则因变量y与自变量x之间的关系式是_____ __________________.
25．若a-b=2, b-c=3, 则a2+b2+c2-ab-bc-ca的值为_________.
26．如图1，在△ABC中，E是AB的中点，D是AC上的一点，且AD∶DC=2∶3，BD与CE交于F， S△ABC=40．一只蚂蚁仅在△ABC上爬行，那么，蚂蚁落在△AＥＤ上的概率是 ___________．
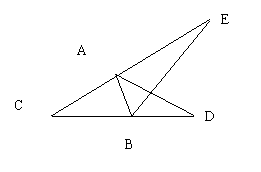
27．如图2已知ΔABC中，∠C=32°，∠A、∠B的外角平分线分别交对边的延长线于D、E两点，且AC=AD，则∠E= _______.
| |||
| |||
二、（本题9分）
29、如图，把一个面积为1的正方形分成两个面积为
的长方形，再把其中一个面积为的长方形分成两个面积为
的正方形，再把其中一个面积为的正方形分成两个面积为
的长方形，如此进行下去，试用图形揭示的规律完成下列各题：
_____________．
三、（本题10分）
29、如图，有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等份，每份分别标上1、2、3、4四个数字；转盘B被均匀地分成6等份，每份分别标上1、2、3、4、5、6六个数字。有人为甲、乙两人设计了一个游戏，其规则如下：(1)同时自由转动转盘A与B；(2)转盘停止后，指针各指向一个数字(如果指针恰好指在分格线上，那么重转一次，直到指针指向某一数字为止)，用所指的两个数字作乘积，如果得到的积是偶数，那么甲胜；如果得到的积是奇数，那么乙胜(如转盘A指针指向3，转盘B指针指向5，3×5=15，按规则乙胜)。你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则，并说明理由。
 |  |
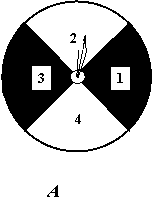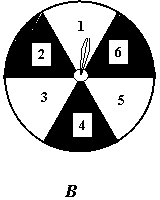四、（本题11分）
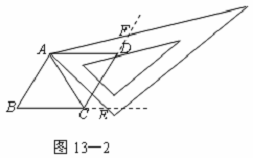
30．用两个全等的等边三角形△ABC和△ACD拼成四边形ABCD.把一个含60°角的三角尺与这个四边形叠合，使三角尺的60°角的顶点与点A重合，两边分别与AB，AC重合.将三角尺绕点A按逆时针方向旋转.
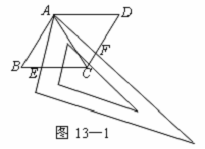（1）当三角尺的两边分别与四边形的两边BC，CD相交于点E，F时，（如图13—1），通过观察或测量BE，CF的长度，你能得出什么结论？并证明你的结论；
（2）当三角尺的两边分别与四边形ABCD的两边BC，CD的延长线相交于点E，F时（如图13—2），你在（1）中得到的结论还成立吗？简要说明理由.
