龙口中心学校七年级数学竞赛试卷
请将第一题的答案代号填入下表中:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
一、选择题（每小题3分，共30分）
1．三角形一个外角小于与它相邻的内角，这个三角形是（ ）
|
C．钝角三角形 D．属于哪一类不能确定
2．一个角的度数是40°，那么它的余角的度数是（ ）．
A．60° B．140° C．50° D．90°
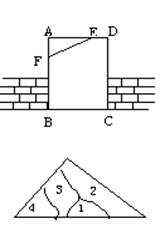
3．如右图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，
使其不变形，这样做的根据是（ ）．
A．两点之间的线段最短 B．长方形的四个角都是直角
C．长方形是轴对称图形 D．三角形有稳定性 （第3题图）
4．小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标
有1、2、3、4的四块），你认为将其中的哪一些块带去，就能
配一块与原来一样大小的三角形? 应该带（ ）．
A．第1块 B．第2 块 C．第3 块 D．第4块 （第4题图）
5.一个长方形在平面直角坐标系中三个顶点的坐标为（– 1，– 1）、
（– 1，2）、（3，– 1），则第四个顶点的坐标为（ ）
A．（2，2） B．（3，2）
C．（3，3） D．（2，3）
6、如右图是汽车行驶速度（千米／时）和时间（分）
的关系图，下列说法其中正确的个数为（ ）
A．1个 B．2个 C．3个 D．4个
（1）汽车行驶时间为40分钟；
（2）AB表示汽车匀速行驶；
（3）在第30分钟时，汽车的速度是90千米／时；
（4）第40分钟时，汽车停下来了． （第6题图）
7．下面各角能成为某多边形的内角和的是（ ）
A．430° B．4343° C．4320° D．4360°
8.同一平面内的四条直线满足a⊥b，b⊥c，c⊥d，则 下列式子成立的是（ ）
A．a∥b B．b⊥d C．a⊥d D．b∥c
9．在平面直角坐标系中，线段A′B′是由线段AB经过平移得到的，已知点A(－2，1)的对应点为
A′(3，4)，点B的对应点为B′(4，0)，则点B的坐标为：（ ）
|
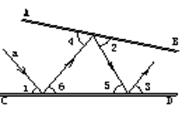
10．如图，光线a照射到平面镜CD上，然后在平面镜AB和
CD之间来回反射，这时光线的入射角等于反射角，即
∠1＝∠6，∠5＝∠3，∠2＝∠4。若已知∠1=55°，
∠3=75°，那么∠2等与（ ）
A．50° B．55° C．66° D．65°
（第10题图）
二、填空题（每小题3分，共30分）
11.在△ABC中，∠A=105°，∠B -∠C=15°，则∠C的度数是_________
12．要从一张长为40cm、宽为20cm的长方形纸片（如图）中，剪出
长为18cm、宽为12cm的长方形纸片，则最多能剪出 张． （第12题图）
13．在直角三角形、钝角三角形和锐角三角形这三种三角形中，有两条高在
三角形外部的是 三角形．
14．把一副常用的三角板如图所示拼在一起，那么图中∠ADE是 度．
15．剧院里5排2号可以用（5，2）表示，则（7，4）表示
16．等腰三角形一边等于5，另一边等于8，则周长是_________
17．点P（-2，1）向上平移2个单位后的点的坐标为
18．一个多边形的每一个外角都等于30°，则这个多边形的边数是 ，它的内角和是
19．已知点A（0，1） ，B（0，2），点C在X轴上，且S△ABC = 4，则C点坐标为
20．已知
，当
时，
的范围是
三、解下列方程组(不等式组)（每小题4分，共16分）
21.
22. 
23．
24.
（并求出最小整数解）
四、解答题：(共44分)
25（5分）关于
的不等式
的解都是不等式
的解，求
的取值范围.
26（4分）如图，有两堵墙，要测量地面上所形成的∠AOB的度数，但人又不能进入围墙，只能站在墙外，如何测量？请运用所学知识说说测量的方法。
27（5分）一辆汽车在行驶的过程中，行驶的路程y（千米）随着行驶时间x（小时）的改变而改变，如果汽车行驶的速度是60千米／小时，请你用适当的方法表示x、y这两个变量之间的关系。
28（４分）如右图，EF∥AD，∠1 =∠2，∠BAC = 70°。将求∠AGD的过程填写完整。
因为EF∥AD，所以 ∠2 = 。
又因为 ∠1 = ∠2，所以 ∠1 = ∠3。
所以AB∥ 。所以∠BAC + = 180°。
又因为∠BAC = 70°，所以∠AGD = 。
29(6分)《一千零一夜》中有这样一段文字：有一群鸽子，其中一部分在树上欢歌，另一部分在地上觅食，树上的一只鸽子对地上觅食的鸽子说：“若从你们中飞上来一只，则树下的鸽子就是整个鸽群的
，若从树上飞下去一只，则树上、树下的鸽子就一样多了。”你知道树上、树下各有多少只鸽子吗？
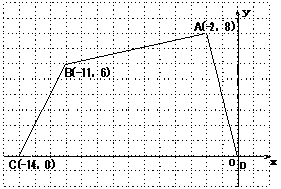
30.(10分)如图四边形ABCD各个顶点的坐标分别为（– 2，8），（– 11，6），（– 14，0），（0，0）
（1）确定这个四边形的面积，你是怎么做的?
（2）如果把原来ABCD各个顶点纵坐标保持不变，横坐标增加2，所得的四边形面积又是多少？为什么?
|
|
图（a） 图（b）
图（c）
（2）若点F在线段AE上（不与A重合），如图（b），此时∠EFD发生变化了吗？为什么？
（3）若点F在△ABC外部，如图（c），此时∠EFD的度数又会怎样变化？为什么？