七年级数学(下)期末测试题(人教版)
(考试时间100分钟,满分100分)
姓名:_______________ 组别:__________ 得分:________________
一、填空(第8小题2分,其余每空2分,共18分)
1、如果b<a,用不等号连接:- ____ - 。 2、如图1,直线AB、BC、
CA分别相交于点A、B、C,画出点A到直线BC的垂线,并量
点A到直线BC距离为______(精确到1cm)。
3、用科学记数表示:-0. = _____________ 。
4、如图2,直线AB、CD、EF交于点O,且AB⊥CD,
如果∠BOF=30°,那么∠EOD=____。
5、在横线上填上适当的式子,使等式成立。
①(3m-n)(_______________________)=27m3 - n3
②(4a- ________)2 =16m2 -40mn+25n2
6、已知线段a,画线段AB=a,延长AB到C,使AC=2a,在AB的反向延长线上取一点E,使
AE= CE,那么CE = _____a。
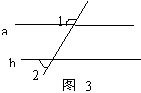
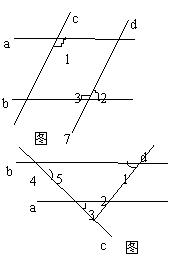
7、如图3,直线a∥b,∠1=115°, 那么∠2=_________。
8、命题“同位角相等,两直线平行”的题设是_____________
______________,结论是__________________________。
二、选择题(每小题2分,共14分)
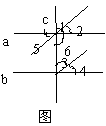
1、如图4,下列判断正确的是( )
A、∠1与∠5是对顶角 B、∠2与∠4是同位角
C、∠3与∠6是同旁内角 D、∠5与∠4是内错角
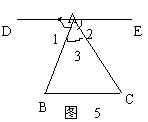
2、如图5,下列推理中正确的是( )
A、∵∠1=∠C∴DE∥BC B、∵∠2 =∠B ∴DE∥BC
C、∵∠BAC +∠C =180° ∴DE∥BC
D、∵∠B +∠2 +∠3 =180° ∴DE∥BC
3、下列计算正确的是( )
A、x2·x3=x6 B、(-c)6÷(-c)4=c2 C、(a+b)2 = a2 + b2 D、[(- )-1-2] 0 = 1
4、下列各题或变形后可以用乘法公式计算的是( )
A、(2a+3b)(3a-2b) B、(m-2n)(m2-2mn+4n2)
C、(x-0.5y)(x2+xy+0.25y2) D、(-a2-1)(a2+1)
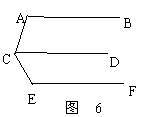
5、如图6,直线AB∥CD∥EF,那么∠A+∠ACE+∠E等于( )
A、180° B、270° C、360° D、540°
6、在同一平面内有5条不同的直线a、b、c、d、e,如果a⊥ b,b∥c,
c⊥d,d∥e,则直线a和直线e的位置关系是( )
A、平行 B、垂直 C、既不平行也不垂直 D、不能确定
7、下列命题是命题的是( )
A、不等式两边都乘以同一个数,不等号的方向不改变
B、互补的两个角中一定是一个是锐角,另一个是钝角
C、两条直线被第三条直线所截,同位角相等
D、两条直线被第三条直线所截,若同位角相等,则同旁内角互补
三、(第1小题5分,第2小题6分,共11分)
1、解不等式组 2、解方程组
四、计算(1、2题各3分,3、4题各4分,共14分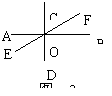
![]()
![]()
![]()
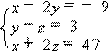
![]()
![]()
![]()
![]()
![]() )
)
1、(x+y)(x2-3xy+y2) 2、2x2y2·(-5x2y)2 ÷5x4y
3、(2a3b6- ab3 )÷(- ab3 ) 4、( )2 + ( )0 + ( )-2
五、计算(能用乘法公式计算的要用乘法公式算,1题4分,2、3题各3分,4题7分,共17分)
1、〔 (x+3y)(x-3y)-(x-3y)2 〕÷6y 2、(-x-2y)(x2-2xy+4y2 )
3、(x-2 )(x4+ 4x2+16 )(x+2 ) 4、先化简再求值:其中a= ,b=-
(a+2b+1 )(-a+2b-1 )(a-1 )。
六、(每小题各4分,共8分)
1、已知:如图7,a∥b,c∥d,∠1=120°。
求∠2、∠3的度数。
2、已知:如图8,∠1与∠3互余,∠2与∠3
的余角互补,∠4=130°,求∠3的度数。
七、(1题5分,2题8分,共13分)
1、在下列括号内,填上适当的依据。
已知:如图9,AD∥BC,∠BAD=∠BCD。
求证:AB∥CD。
证明:∵AD∥BC( )
∴∠1= _______( )
又∵∠BAD=∠BCD( )
∴∠BAD-∠1=∠BCD-∠2
即∠3=∠4
∴AB∥CD( )
2、列方程组解应用题
甲、乙两人从相距18公里的两地同时出发,相向而行2小时相遇;如果甲比乙先出发3 小时,
那么乙出发后1小时两 人相遇。求两人的速度各 是多少?
 | |||||||
 | |||||||
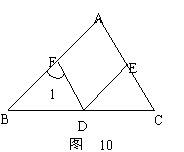 | |||||||
八、(5分)已知:如图10,D、E、F分别是BC、CA、AB上的点,
DE∥AB,DF∥CA。
求证:∠EDF=∠A(写出证明过程,并注明各步理由)