第五章 三角形 复习
一、知识点：
1、三角形的三边关系：①三角形任意两边之和 第三边；②三角形任意两边之差 第三边。下列每组分别是三根小木棒的长度，用它们能摆成三角形吗？（单位：厘米。填“能”或“不能”） （1）3，4，5（ ）
（2）8，7，15（ ） （3）13，12，20（ ） （4）5，5，11（ ）
2、三角形三个内角的和等于 °。
在△ABC中，∠C=70°，∠A=50°，则∠B= 度；
3、三角形按内角的大小分为三类：①锐角三角形；②直角三角形；③钝角三角形。一个三角形两个内角的度数分别如下，这个三角形是什么三角形？
（1）30°和60° （ ）
（2）40°和70° （ ）
（3）50°和30° （ ）
4、直角三角形的两锐角 。
如上图， 在Rt△ABC中，∠A=2∠B，则∠A= 度，∠B= 度；
5、三角形的三条角平分线交于
，三条中线交于 ，三条高所在的直线交于 。三角形的角平分线、中线、高都是 （填“直线”、“射线”或“线段”）如图，在△ABC中，
（1）AD是中线，那么BD＝ ＝
，
BC＝ BD＝ DC；
（2）AE是角平分线，那么∠BAE＝ ＝ ，
∠BAC＝ ∠BAE＝ ∠EAC；
（3）AF是BC边上的高，那么∠AFB＝∠AFC＝ °，AF BC。
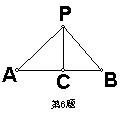6、两个能够重合的图形称为
；
全等图形的 和 都相等；
全等三角形的对应边 ，对应角 。
如图；△ACP≌△BCP，那么
，
7、三角形全等的条件：
①三边对应相等的两个三角形全等，简写成 或
②两角和它们的夹边对应相等的两个三角形全等，简写成 或
③两角和其中一角的对边对应相等的两个三角形全等，简写成 或
④两边和它们的夹角对应相等的两个三角形全等，简写成 或
8、直角三角形全等的条件：斜边和一条直角边对应相等的两个直角三角形全等，简写成 或
二、巩固练习：（一）填空：
1、在△ABC，AB＝5，BC＝9，那么 ＜AC＜
2、一个三角形的两边长分别是3和8，而第三边长为奇数，那么第三边长是
3、已知一个等腰三角形的一边是3cm，一边是7cm，这个三角形的周长是
 |  | ||
（第4题） （第5题）
4、如上图，∠1=60°，∠D=20°，则∠A= 度
5、如上图，AD⊥BC，∠1=40°，∠2=30°，则∠B= 度，∠C= 度
6、已知△ABC中，∠A∶∠B∶∠C=1∶2∶3，则∠A＝ 度，∠B＝ 度∠C＝ 度。
7、在空白处填入“锐角”、“直角”或“钝角”：
（1） 如果三角形的三个内角都相等，那么这个三角形是 三角形；
（2）如果三角形的两个内角都小于40°，那么这个三角形是 三角形。
8、（1）已知：如图，AD∥BC，AD＝CB，你能说明△ADC≌△CBA吗？
证明： ∵AD∥BC（已知）
∴
（两直线平行，内错角相等）
在 中
∴ ≌ （ ）
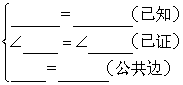
（2）如图，∠B＝∠C ，AD平分∠BAC，你能证明△ABD≌△ACD？
证明：∵AD平分∠BAC（ ）
∴∠ ＝∠ （角平分线的定义）
在△ABD和△ACD中
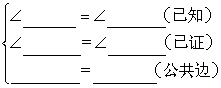
∴△ABD △ACD（ ）
（二）解答题：
1、如图，已知AB＝AC，AD是BC边上的中线，你能说明AD是角平分线吗？
证明：∵AD是BC边上的中线（已知）
∴ ＝ （中线的定义）
在 中
∴ ≌ （ ）
∴ ＝ （全等三角形的对应角相等）
∴AD是角平分线（ ）
2、如图，已知AB＝AC，AE＝AD，∠1＝∠2，你能说明△ABD≌△ACE吗？
 |
3、如图，要量河两岸相对两点A、B的距离，可以在AB的垂线BF上取两点C、D，使CD=BC，再定出BF的垂线DE，使A、C、E在一条直线上，这时测得DE的长就是AB的长，试说明理由。
 |
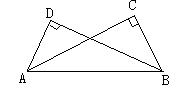
4、如图，AD＝BC，∠D＝∠C＝90°，△ABD和△BAC全等吗？
5、尺规作图：（1）已知三角形的两角及其夹边，求作这个三角形.
已知：线段∠α，∠β，线段a 。
求作：ΔABC，使得∠A=∠α，∠B=∠β，AB=a。
（2） 已知三角形的两边及其夹角，求作这个三角形.
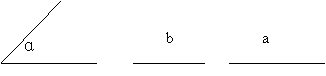已知：
求作：
7、请用全等图形设计一个你自己认为满意的图案。