浙教版七年级上册同步练习 7.7 相交线（1）
[基础训练]
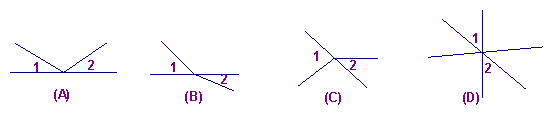
1、下列各图中，∠1和∠2是对顶角的是 （ ）
2、两条直线相交只有 个交点。
3、对顶角 。
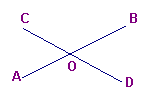
4、如图，直线AB、CD相交于点O，若∠AOC=50度，
则∠BOC= ，∠AOD= ∠BOD= 。
|
5、如图，直线AB与CD相交于点O，射线OE平分
∠AOC，已知∠AOD=40度，则∠COE= ，
∠BOD= 。
6、若∠1与∠2是对顶角，∠3与∠2互余，且∠3=60度，
那么∠1=
。
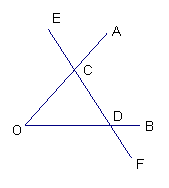
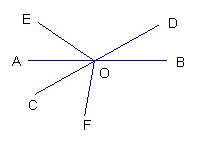
7、如图，直线EF交∠AOB于C、D两点，请说明如图中的对顶角。
8、如图，直线AD和BE相交于O点，∠COD=90度，∠COE=70度，
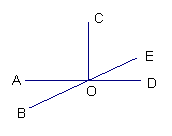求∠AOB的度数。
[综合提高]
一、选择题
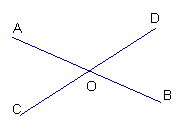
1、已知直线AB、CD相交于点O，则与∠AOC互补的角有 （ ）
A、1个 B、2个 C、3个 D、4个
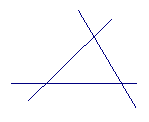
2、如图，三条直线两两相交，其中对顶角共有 ( ）
A、3对
B、4对 C、5对 D、6对
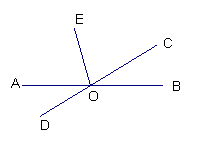
3、如图，直线AB、CD交于点O，OE、OF是过O点的两条射线，其中构成对顶角的是 （ ）
A、∠AOF与 ∠DOE B、∠EOF与∠BOE
C、∠BOC与∠AOD D、∠COF与∠BOD
4、下列说法错误的是 （ ）
A、对顶角的平分线成一个平角 B、对顶角相等
C、相等的角是对顶角
D、对顶角的余角相等
5、如图，直线AB与CD相交于点O，∠AOD+∠BOC=236度，则∠AOC的度数为 （ ）
A、72度 B、62度 C、124度 D、144度
二、填空题
6、若∠1与∠2是对顶角，且∠1与∠2互余，则∠1=_____，∠2=_____。
7、如图，直线AB、CD交于点O，OE平分∠AOC，
若∠AOD=50度，则∠BOE=____________。
8、如图，直线AB、CD交于点O，则
（1）若∠1+∠3=68度，则∠1=
。
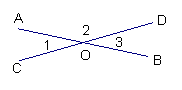（2）若∠2：∠3=4：1，则∠2=
。
（3）若∠2-∠1=100度，则∠3= 。
三、解答题：
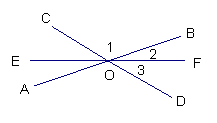9、已知直线AB、CD、EF相交于点O，∠1：∠3=3：1，
∠2=20度，求∠DOE的度数。
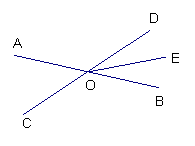
10、如图，直线AB、CD相交于点O，OE平分∠BOD，且∠AOC=∠AOD-80度，求∠AOE的度数。
[探究创新]
三条直线相交于一点，能构成几对对顶角、？四条呢？五条呢？n条呢？
浙教版七年级上册同步练习7.7 相交线（2）
[基础训练]
1、如果两条直线互相垂直，那么这两条直线相交所成的角是 （ ）
A、直角 B、锐角 C、任意一个角 D、钝角
2、下列说法中，不正确的是 （ ）
A、一条直线的垂线有无数条 B、一条直线只有一条垂线
C、过一点可画多条直线的垂线 D、过一点画直线的垂线，垂足必有直线上
3、过一点 一条直线与已知直线垂直。
4、如果两条直线相交成直角，那么这两条直线 ，它们的交点叫做 。
5、过点A作直线L的垂线，垂足为B点，线段AB的 叫做点A到直线L的距离。
6、在阳光下，学校里的旗杆与它在地上的影子的位置关系是 。
7、按下列要求画垂线。
B
. M
A .N
（1）画一条与AB垂直的直线，这样的垂线可以画几条？
（2）过直线AB上的点M，画AB的垂线，这样的垂线有几条？
（3）过直线AB外一点N，画AB的垂线，这样的垂线有几条？
8、举出生活中两条垂直线段的例子，与同学讨论垂直这一知识在实际生活中的意义。
[综合提高]
一，选择题
1、过一条线段外一点画线段的垂线，垂足在 （ ）
A、这条线段上 B、这条线段的端点上
C、这条线段的延长线上 D、以上三种都有可能
2、和一个已知点P距离等于3厘米的直线可画 （ ）
A、1条 B、2条 C、3条 D、无数条
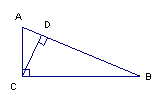
3、如图，点A到直线CD的距离是指哪条线段长 （ ）
A、AC B、CD C、AD D、BD
4、在“同一平面内，过一点有且只有一条直线与已知直线垂直”中这一点的位置 （ ）
A、在直线的上方 B、在直线的下方 C、在直线上 D、可以任意位置
5、下列说法中正确的个数有 （ ）
（1）直线外一点与直线上各点连接的所有线中垂线段最短。
（2）画一条直线的垂线段可以画无数条。
（3）在同一平面内，经过一个已知点能画一条且只能画一条直线和已知直线垂直。
（4）从直线外一点到这条直线的垂线段叫做点到直线的距离。
A、1个 B、2个 C、3个 D、4个
6、已知∠AOB=30度，OC⊥OA，OD⊥OB，则∠COD= （ ）
A、30度 B、90度 C、150度 D、30度或150度
二、填空题
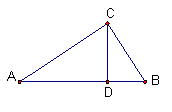
7、如图，互相垂直的线段有 _________________________ 。
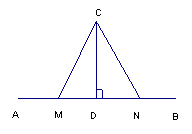
8、如图，C点是直线AB外一点，过点C画CD⊥AB，垂足为D，M、N是AB上异于点D的两点，连结CM、CN，量出CD、CM，CN的长度，则 最短。
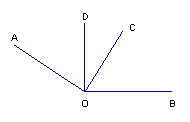9、过钝角的顶点在角的内部作一边的垂线，若这条垂线把这个角分成3：2的两部分，则这个角的大小为
。
10、如图，AO⊥OC，DO⊥OB，∠AOD=50度，则∠BOC= 。
11、在同一平面内有两个角，而且这两个角的两边分别垂直，
则这两个角的大小关系是 。
三、解答题
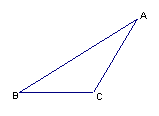
12、如图，过三角形ABC的三个顶点A、B、C，分别
作BC、AC、AB的垂线，并用“⊥”符号表示出来。
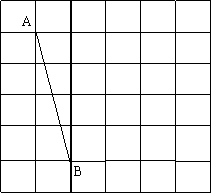
13、如图，在正方形的网格中，只用直尺画出线段CD，使CD⊥AB。
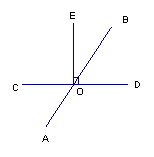14、如图，两直线AB、CD相交于O点，OE⊥CD，且∠BOE=1/3∠BOC，试求∠AOC的度数。
[探究创新]
12点正时针和分针重合，经过几分钟时针与分针第一次垂直。
7.7 相交线（1）
基础训练：
1 . D 2 . 1 3 .相等 4.130º, 130º，50º ； 5. 70º; 140º 6 .30º 7. ∠ACE与 ∠∠OCD，∠ACD 与∠ECO，∠CDO 与∠BDF，∠CDB与∠ODF ； 8. 20º
综合提高：
一．选择题：
1 B 2. D 3. C 4. C 5. B
二．填空题：
6．45º，45º 7. 115º 8.⑴ 34º, （2）144º （3）40º;
三．解答题：
9．140 º 10 . 155º
探究创新：
6对，12对，20对，（n2 -n）对
7.7 相交线（2）
基础训练：
1 . A 2 . B 3 .有且只有; 4.互相垂直，垂足 ； 5. 长 6 . 互相垂直 7. （1）无数条 ；（2）一条（3）一条 8. 略
综合提高：
一．选择题：
1 D 2. D 3. C 4. D 5. C 6 . D
二．填空题：
7． AC与BC， AB与 CD 8. CD 9.150º 10.50º 11. 相等或互补
三．解答题：
12. 略 13.略 14.45º
探究创新：
180/11分钟