张家口市高新区2005～2006学年第一学期期中考试
七年级数学试题
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 总 分 |
| 1-10 | 11-20 | 21-24 | 25-26 | 27 | 28 | 29 | 30 | ||
| 得分 |
注：1、可以使用计算器，但未注明精确度的计算问题不得采取近似计算，建议根据题型的特点把握好使用计算器的时机。
2、本试卷满分100分，在90分钟内完成。
| 得 分 | 评卷人 |
一、选择题（本题共10小题，每小题2分，共20分。每小题给出4个答案，其中只有一个是正确的，请把选出的字母编号填在题后的括号中，否则不给分）
1．
的值是（ ）
（A）－2 （B）2 （C）4 （D）－4
2． 冬季某天我国三个城市的最高气温分别是－10℃、1℃、－7℃，把它们从高到低排列正确的是（ ）
（A）－10℃、－7℃、1℃ （B）－7℃、－10℃、1℃
（C）1℃、－7℃、－10℃ （D）1℃、－10℃、－7℃
3．
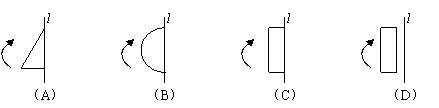如图所示，下列图形绕直线l旋转360°后，能得到圆柱体的是（ ）
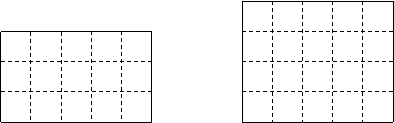
4． 某物体的三视图如右图所示，那么该物体的形状是（ ）
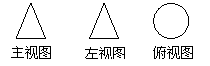（A）长方体
（B）圆锥体
（C）正方体 （D）圆柱体
5． 在长方体的截面中，边数最多的截面是（ ）
（A）四边形 （B）五边形 （C）六边形 （D）七边形
6． 某种细胞开始有2个，1小时后分裂成4个并死1个，2小时后分裂成6个并死1个，3小时后分裂成10个并死1个，……，6小时后细胞存活的个数是（ ） （A）63 （B）65 （C）67 （D）71
7．
右边给出的是2004年3月份的日历表，任意圈出一竖列上相邻的三个数，请你运用所学知识来研究，发现这三个数的和不可能是（ ）
（A）69 （B）54
（C）27 （D）40
第1页，共6页
8．
图1是由白色纸板拼成的立体图形，将此立体图形中的两面涂上颜色，如图2所示．下列四个图形中哪一个是图2的展开图？（ ）
 |
9．
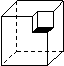如图，从边长为10的正方体的一顶点处挖去一个边长为1的小正方体，则剩下图形的表面积为（ ）
（A）600 （B）599 （C）598 （D）597
10．一杯可乐售价1.8元，商家为了促销，顾客每买一杯可乐获一张奖券，每三张奖券可兑换一杯可乐，则每张奖券相当于（ ）
（A）0.6元 （B）0.5元 （C）0.45元 （D）0.3元
| 得 分 | 评卷人 |
二、填空题（本题共10小题，每小题2分，共20分。请将最终答案填在题中的横线上）
11．
的相反数的倒数是
；
12．如果节约20千瓦·时电记作＋20千瓦·时，那么浪费10千瓦·时电记作 ；
13．计算：－（－2）3＝ ；－a2b－2ba2＝ ；
14．数轴上点A表示数－3，则与点A相距2个单位长度的点所表示的数是 ；
15．
使用计算器进行计算时，按键程序为 － 8 ×
5 ÷
4 ＝
，则结果为
；
16．礼堂第一排有a个座位，后面每排都比第一排多1个座位，则第n排座位有 个；
17．如图，阴影部分的面积用代数式表示为 ；
18．计算：1－2＋3－4＋5－6＋…＋2003－2004＋2005＝ ；
19．现有四个有理数3，4，－6，10，将这四个数（每个数用且只用一次）进行加减乘除四则运算，使其结果等于24．请你写出一个符合条件的算式： ；
20．
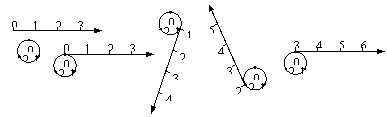如下图所示，按下列方法将数轴的正半轴绕在一个圆上（该圆周长为3个单位长，且在圆周的三等分点处分别标上了数字0、1、2）上：先让原点与圆周上数字0所对应的点重合，再将正半轴按顺时针方向绕在该圆周上，使数轴上1、2、3、4、…所对应的点分别与圆周上1、2、0、1、…所对应的点重合．这样，正半轴上的整数就与圆周上的数字建立了一种对应关系．
⑴圆周上的数字a与数轴上的数5对应，则a＝ ；
⑵数轴上的一个整数点刚刚绕过圆周n圈（n为正整数）后，并落在圆周上数字1所对应的位置，这个整数是 （用含n的代数式表示）．
第2页，共6页
| 得 分 | 评卷人 |
三、试试基本功（本题共4小题，共16分）
21．
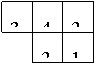如图，是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，请你画出这个几何体的主视图和左视图．（4分）
22．计算：－20.02×（2.15－2）÷2005＋（－1）2005＋│－12005│；（4分）
23．计算：25×
―（―25）×
＋25×（－
）；（4分）
24．先化简，再求值：2（a2b＋ab2）－2（a2b－1）－2 ab2－2，其中a＝－2，b＝3．
（4分）
| 得 分 | 评卷人 |
四、归纳与猜想（本题共2小题，共11分）
25．下面是用棋子摆成的“上”字：
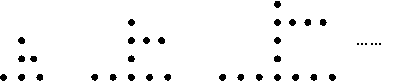
第一个“上”字 第二个“上”字 第三个“上”字
如果按照以上规律继续摆下去，那么通过观察，可以发现：
⑴第四、第五个“上”字分别需用 和 枚棋子；（2分）
⑵第n个“上”字需用 枚棋子．（2分）
第3页，共6页
26．如图，①、②、③、④四个图都称作平面图，观察图①和表中对应数值，探究计数的方法并作答：
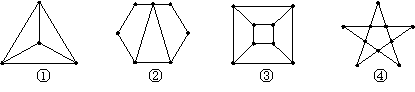
⑴数一数每个图各有多少个顶点，多少条边，这些边围出多少区域，并将结果填入下表：（3分）
| 图 | ① | ② | ③ | ④ |
| 顶点数（V） | 4 | |||
| 边数（E） | 6 | |||
| 区域数（F） | 3 |
⑵根据表中数值，写出平面图的顶点数V、边数E、区域数F之间的一种关系：
答： ；（2分）
⑶如果一个平面图由20个顶点和11个区域，那么利用⑵中得出的关系，求这个平面图有多少条边？（2分）
| 得 分 | 评卷人 |
五、观察与判断（本题共8分）
27．下表是小明记录的今年雨季流花河一周内的水位变化情况：
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 水位变化/米 | ＋0.20 | ＋0.81 | －0.35 | ＋0.03 | ＋0.28 | －0.36 | －0.01 |
（注：正号表示水位比前一天上升，负号表示水位比前一天下降）
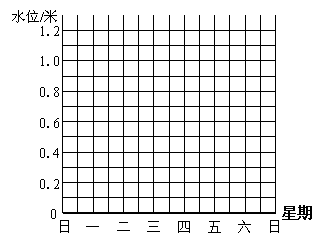⑴若上周末的水位记为a米，请用含a的代数式表示本周星期三的水位；
⑵以上周末的水位为0点，用折线统计图表示本周水位变化情况；
⑶请判断本周七天内水位最高的是哪天，最低的是哪天？它们相差多少？
⑷与上周末相比，本周末河流的水位变化了吗？是如何变化的？
第4页，共6页
| 得 分 | 评卷人 |
六、实验与拓广（本题共6分）
28．
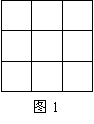“九宫图”传说是远古时代洛河中的一个神龟背上的图案，故又称“龟背图”，中国古代数学史上经常研究这一神话。
⑴现有1，2，3，4，5，6，7，8，9共九个数字，请将它们分别填入右图1的九个方格中，使得第行的三个数、每列的三个数、斜对角的三个数之和都等于15．
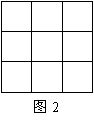⑵通过研究问题⑴，利用你发现的规律，将3，5，－7，1，7，－3，9，－5，－1这九个数字分别填入右图2的九个方格中，使得横、竖、斜对角的所有三个数的和都相等．
| 得 分 | 评卷人 |
七、应用与说理（本题共7分）
29．某学习小组四个同学在探讨问题：
小明说：“请你们任想一个整数，将这个数乘以2加7，把结果再乘3减21，这个数一定是6的倍数！”
⑴请你写出一个数，并按小明的规则，验证一下是否正确；
⑵若正确，请你用所学的数学知识说明理由；若不正确，请改正．
第5页，共6页
| 得 分 | 评卷人 |
八、操作与探究（本题12分）
30．如图1所示的图形是由5个正方形相连组成的，它可以折成一个无盖的立方体盒子，如图2所示．
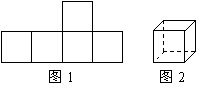⑴由五个正方形相连可组成各种不同的图形，试将这种图形尽可能多地画出来；（要求至少画出4种）
⑵在你所画的图形中，哪些可以折成一个无盖的立方体盒子？（要求至少找到3种，如果你能再找到多余3种以上的图形，可给予适当的加分，但总分不超过100分）
⑶如图，有两个3×5和4×5的长方形，你能利用这两个长方形做出多少个无盖的立方体盒子？当然，要求这些盒子的每个面的大小刚好等于图中的小正方形的大小．请你把要剪开的线段用实线画出．
第6页，共6页
张家口市高新区2005～2006学年第一学期期中考试
七年级数学试题参考答案
一、选择题：
1、C 2、C 3、C 4、B 5、C 6、B 7、D 8、A 9、A 10、C
二、填空题：
11、2 12、－10千瓦·时 13、8 ，－3a2b 14、―5或―1 15、－10
16、（a＋n－1） 17、2ab－8 18、1003 19、如3×（－6＋4＋10）＝24
20、2 ，3n＋1
三、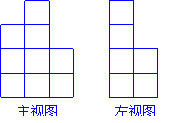
试试基本功：
21、解：各2分，共4分
22、解：∵2.15－2＝0， 2分
∴原式＝0－1＋1＝0． 4分
23、解：原式＝25×－25×＋25× 1分
＝25×（－＋） 3分
＝25×1＝25 4分
24、解：原式＝2a2b＋2ab2－2a2b＋2－2 ab2－2 2分
＝（2－2）a2b＋（2－2）ab2＋（2－2）
＝0 3分
∴当a＝－2，b＝3时，原式＝0． 4分
四、归纳与猜想：
25、⑴18 ，22 （2分）
⑵4n＋2 （4分）
26、⑴
| 图 | ① | ② | ③ | ④ |
| 顶点数（V） | 4 | 7 | 8 | 10 |
| 边数（E） | 6 | 9 | 12 | 15 |
| 区域数（F） | 3 | 3 | 5 | 6 |
3分
⑵V＋F－1＝E 5分
⑶30 7分
五、观察与判断：
27、⑴解：a＋0.20＋0.81－0.35，即a＋0.66（2分）
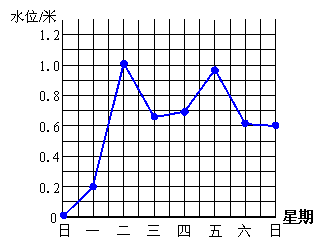⑵如图，（4分）
⑶解：水位最高的是星期二，最低的是星期一，它们相差0.81米；（6分）
⑷答：与上周末相比，本周末的水位变化了，且水位上升了。（8分）
六、实验与拓广：
28、各3分，共6分
 |  |
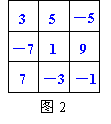七、应用与说理：
29、解：⑴若这个整数为1，则（1×2＋7）×3－21＝6； 2分
故，小明所说的结论正确； 3分
⑵设这个整数为a，则
（a×2＋7）×3－21 5分
＝3（2a＋7）－21
＝6a＋21－21＝6a 6分
∴6a一定是6的倍数。 7分
八、操作与探究：
30、解：⑴（答案不唯一，但尽可能多，现给出12种，画出4种以上，得4分）
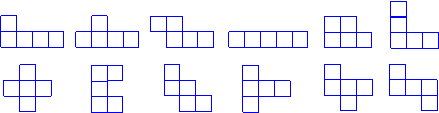
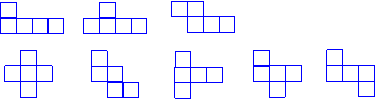
⑵要判断这些图形是否可以折成一个无盖的立方体盒子，需要一定的空间想象力，在以上的12种图形中，下面8种都可以折成一个无盖的立方体盒子。学生画出3种得3分，每多画一种多加1分。
⑶指出共可做出7个无盖的立方体盒子，得1分．画出每个图形的实线段各占2分，本小问共计5分。如图，“┳”型是其中一种裁剪方法。当然，还有其它方法。
