第四章 代数式（综合）
班级 学号 姓名 成绩
一、填空题（每空2分，共32分）
1、用代数式表示：（1）温度由24°C下降t°C后是 °C；
（2）边长为a的正方形的面积为 。
2、当x =-2时，代数式
的值是
。
3、单项式
的系数是
；当r=3时，这个代数式的值是
。
4、多项式
是
次
项式。
5、说出一个可以用
表示结果的实际问题：
。
6、合并同类项：
；
。
7、去括号：
；
。
8、化简：
。
9、一种商品每件成本a元，按成本增加22%定出标价，那么这种商品每件的标价是 元，后因库存积压减价，商品按标价的八五折（85%）出售，那么打折后每件的售价为 元。
10、甲乙两地相距s千米，小明从甲地骑车到乙地要t 小时，如果要求他提前1小时到达乙地，那么小明骑车的速度应为 千米/小时。
二、选择题（每小题3分，共24分）
11、用字母表示数，下列书写规范的是（ ）
A、
B、
C、
D、
12、“a与5 的差的
”可表示为（ ）
A、
B、
C、
D、
13、关于单项式
的系数和次数，下列说法，正确的是（ ）
A、系数为0，次数为2 B、系数为0，次数为4
C、系数为1，次数为2 D、系数为1，次数为4
14、代数式
的意义是（ ）
A、a除以b加1 B、b加1除a C、b与1的和除以a D、a除以b与1的和所得的商
15、当x分别取1和-1时，代数式
的值（ ）
A、相等 B、互为相反数 C、互为倒数 D、以上都不对
16、下列各组代数式中，两个项是同类项的是（ ）
A、2a与a2 B、5a2b与a2b C、2xy与x2y D、0.3mn2与0.3xy2
17、不改变
的值，把它括号前的符号改成相反的符号应为（ ）
A、
B、
C、
D、
18、设x表示一个一位数，y表示一个两位数，现将x放在y的左边组成一个三位数，可以表示为（ ）
A、100x+y B、10x+y C、x+y D、xy
三、解答题（共44分）
19、（8分）用代数式表示：
（1） a的平方与b的2倍的差；
（2）x与y的差的绝对值减去x 与y的积；
（3）每本练习本售价x元，小红买了9本，小慧买了6本，两人一共花了多少元钱？
（4）在学校举行的秋季运动会上，小明和小华进行800米比赛，小明用了x秒跑完全程，小华用了y秒跑完全程，如果小华先到达终点，那么小华比小明每秒多跑几米？
20、（12分）计算：
（1）
（2）
（3）
（4）
（5）
（6）
21、（8分）先化简，后求值：
（1）
，其中x=2;
(2)
，其中a=2，b= -3。
22、（4分）三角形的一边长为a+b，第二边比第一边大a-5，第三边等于2b。
（1） 求三角形的周长；
（2） 当a=6,b=3进，求这个三角形周长的值。
23、（4分）人在运动时的心跳速率通常和人的年龄有关，如果用a表示 一个人的年龄，b表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数，那么有b=0.8(200-a)。请问，一个45岁的人运动时10秒心跳次数为22次，他有危险吗？
24、（8分）将连续的偶数2，4，6，8，10，12，……排列成如下的数表，解答下列问题：
（1）十字框中的五个数的和与中间的数16有什么关系？
（2）设中间的数为a，用代数式表示十字框中的五个数之和；
（3）如果将十字框上下左右平移，可框住另外五个数，试问这五个数还有这种规律吗？
（4）十字框中的五个数之和能等于2005吗？如果能，请你写出这五个数；如不能，请说明理由。
2 4 6 8 10
12 14 16 18 20
22 24 26 28 30
32 34 36 38 40
四、能力拓展题（附加20分）
25、（10分）（1）已知
，求
的值；
（2）如果关于字母x的代数式
的值与x的取值无关，求m、n值。
 |
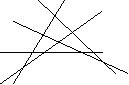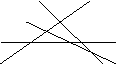
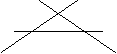26、（10分）如图，下列直线两两相交。
 |
（1）数一数，这四个图形中交点的个数，它们依次是 ， ， ， 。
（2）你认为，当6条直线两两相交，最多有几个交点？当n条直线两两相交时，最多有几个交点？
（3）试计算当100条直线两两相交时，最多有几个交点。
一、24-t，a2，2、5，3、2π/3，6π，4、二，四，5、略，6、-7a/2，-2x2y，7、-a+b，-6x+3y，8、x+y，9、122%a，103.7%a，10、s/(t-1)，二、11—14：BCDD，15—18：ABCA，三、19、a2-2b，
，15x，800/x-800/y，20、8a，
，21、
，22、3a+4b-5，25，23、45岁的人每分钟所能承受的最高124次，即10秒内所能承受的最高次为20.7次，有危险。24、等于16的5倍，5a，仍有这种规律，不能，因为当5a=2005时，a=401不是偶数。四、能力拓展题：25、38，m=1，n=3，26、1，3，6，10， 15个，1/2(n(n-1))，4950。