北环中学2003——2004学年第二学期期末考试（B卷）
七年级数学试卷
命题人：丛淑萍 2004。6。20
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | 总 分 | |||||
| 1-10 | 11-20 | 21-24 | 25-26 | 27 | 28 | 29 | 30 | |||||
| 得分 | ||||||||||||
本试卷满分100分，在90分钟内完成。相信你本次的表现更加出色！
一、请你精心选一选：（本题共10小题，每题2分，共20分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
每题给出4个答案，其中只有一个是正确的，请把选出的答案编号填在上面的答题表中，否则不给分.
1．国旗是一个国家的象征，观察下面的国旗，是轴对称图形的是（ ）
A.加拿大、哥斯达黎加、乌拉圭 B.加拿大、瑞典、澳大利亚
C.加拿大、瑞典、瑞士 D.乌拉圭、瑞典、瑞士
加拿大 哥斯达黎加 澳大利亚 乌拉圭 瑞典 瑞士
2．下列说法：①
；② 用小数表示
为
；③
④
其中正确的有( )
A、1个 B、 2个 C、3个 D、4个
3.下列计算中，正确的是 （ ）
A．
B．
C．
D．
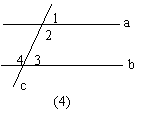
4．如图，不一定能推出a∥b的条件是 ( )
A、∠1＝∠3 B、∠2＝∠4 C、∠1＝∠4 D、∠2＋∠3＝180º
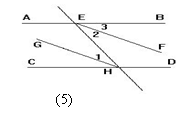
5.如图，若EF∥GH，则 ( )
A. ∠BEH＝∠CHE ; B. ∠1＝∠2 C. ∠1＝∠3 D. ∠BEF＝∠CHG
6．、等腰三角形的周长为13cm，其中一边长为3cm，则该等腰三角形的底边长为（ ）
A、7cm B、3cm C、7cm或3cm D、5cm
7．下列语句正确的是 （ ）
A． 近似数0.009精确到百分位.
B． 近似数800精确到个位,有一个有效数字.
C． 近似数56.7万精确到千位,有三个有效数字.
D． 近似数
精确千分位.
8．如图，⊿ABC中，CD⊥BC于C，D点在AB的延长线上，则CD是⊿ABC（ ）
A、BC边上的高 B、AB边上的高 C、AC边上的高 D、以上都不对
9．如图，已知AB=AC，E是角平分线AD上任意一点，则图中全等三角形有（ ）
A、4对 B、3对 C、2对 D、1对
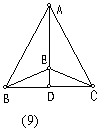
1
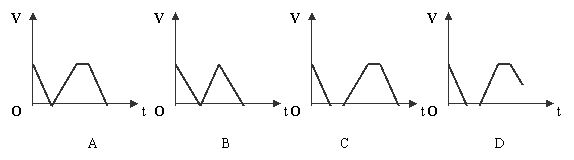
10．有一游泳池注满水，现按一定的速度将水排尽，然后进行清扫，再按相同的速度注满清水，使用一段时间后，又按相同的速度将水排尽，则游泳池的存水量V（立方米）随时间t（小时）变化的大致图象可以是 （ ）
二、请你耐心填一填：（共10小题，其中第18题3分，第20题4分，其余每题2分，共23分，请将答案填入答题表中）
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 答案 | |||||
| 题号 | 16 | 17 | 18 | 19 | 20 |
| 答案 | ⑴ | ||||
| ⑵ |
11．已知
是关于
的一个单项式，且系数是5，次数是7，那么
，
。
12． 
；
.
13．一个正方体的棱长为2×102毫米，用科学计数法表示：它的表面积= 平方米，它的体积= 立方米。
14．小明照镜子的时候，发现T恤上的英文单词在镜子中呈现“
”的样子，
请你判断这个英文单词是 。
15．若等腰三角形的一个角是另一个角的2倍，则它的底角是 ，该三角形的对称轴是 。
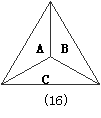
16．如图，是一个正三角形的靶子，靶心为其三条对称轴的交点，则A部分面积占靶子面积的 ，飞镖随机地掷在靶上，则投到区域A或区域B的概率是 。
17．如图，如果
，
，那么
≌
，根据是
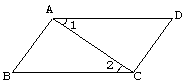
(17)
18．如图，已知∠ABC=∠DCB，现要证明ΔABC≌ΔDCB，则还要补加一个条件
或 ，或 。
19．如图，请在下面这一组图形符号中找出它们所蕴涵的内在规律，然后在横线上的空白处填上恰当的图形。
20.如图,用黑白两色正形瓷砖铺设矩形地面,请观察下图并解答有关问题：
⑴．在第ｎ个图中，每一横行共有 块瓷砖,每一竖列共有 块瓷砖,白色瓷砖共有 块；（用含n的代数式表示）
⑵．设铺设地面所用瓷砖的总块数为y，请写出y与⑴中的n的关系式：
三、请你细心算一算：（共4题，其中第21-23题每题5分，第24题6分,共21分）
21．
22．
解：原式= 解：原式=
23．
(利用乘法公式计算)
解：原式=
24．利用你所学的知识判断
与字母x、y谁的取值无关？然后找一个你喜爱的数代入求出这个代数式的值。
四.看谁画得好! （共2题，每题5分，共10分）
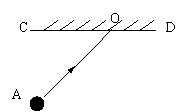
25.如图：打台球时，小球由A点出发撞击到台球桌边CD的点O处，请用尺规作图的方法作出小球反弹后的运动方向（不写作法，但要保留作图痕迹）(5分)
 |
26.公路AB的同侧有工厂C和D，要在公路AB上建一个货场P，使得两个工厂C和D到货场P的距离之和最小，请你在图中作出点P.（不写作法，但要保留作图痕迹）(5分)
五.看谁说得好! （共3题，27、29每题6分,28题8分.共20分）
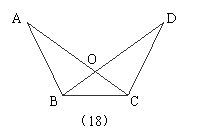
27．如图（1），A，B两个建筑物分别位于河的两岸，要测得它们之间的距离，可以从B出发沿河岸画一条射线BF，在BF上截取BC=CD，过D作DE∥AB，使E，C，A在同一条直线上，则DE的长就是A，B之间的距离。请你说明道理。你还能想出其他方法吗？请把你的设计画在图（2）上。 (6分)
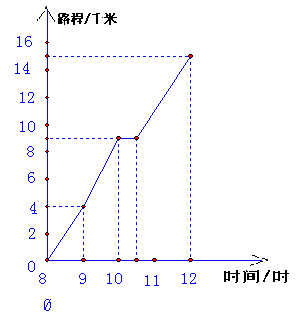28．图为一位旅行者在早晨８时从城市出发到
郊外所走的路程与时间的变化图。
根据图回答问题。(8分)
(1).图象表示了那两个变量的关系？哪个
是自变量？哪个是因变量？
（2） .9时，１０时３０分，１２时所走
的路程分别是多少？
(3).他休息了多长时间？
(4).他从休息后直至到达目的地这段
时间的平均速度是多少？
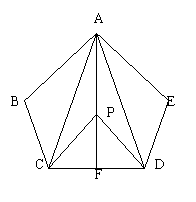29．如图，AB=AE，∠B=∠E，BC=ED，F是CD的中点，
（1） AC与AD相等吗？为什么？
（2） AF与CD的位置关系如何？说明理由。
（3） 若P为AF上的一点，那么PC与PD相等吗？
为什么？（6）
五.看谁更有创意! （6分）
30.请用一个等腰三角形、两个矩形、三个圆，设计一个轴对称图形，并用简练的文字说明你的创意。
北环中学2003——2004第二学期期末七年级数学参考答案
一．选择题（A、B、C卷同）
C A C C B B C D B C
二．填空题（A、B、C卷同）
11．-5，6 12.
,1
13.
,
14.APPLE 15.72°或45°，底边的中垂线（或底边的中线、底边上的高、顶角的平分线所在的直线）
16．
，
17.SAS 18.AB=DC,∠A=∠D,∠ACB=∠DBC 19.
20.(1) n+3 ,n+2 ,n(n+1) (2)y=(n+3)(n+2) (或y=n2+5n+6).
三.(A卷)
21.
22.-C2 23. 0.
四.(A卷)
24.略。
25.证ΔABC≌ΔEDC.设计方法:作射线BF⊥AB,在BF上取两点C、D使BC=CD,过D作DE⊥BF,使E、C、A三点在一条直线上，则DE的长就是A、B之间的距离。
26．（1）表示了时间与距离的关系，时间是自变量，路程是因变量。
（2）4km，9km，15km 。
（3）30分钟
（4）4km/时
27.略.
28.(1)略.(2)BD=DE+CE (3)BD=DE-CE 略
29.略.
三.(B卷)
21. 
22.
23.1 24 –y 略.
四. (B卷) 25 略26.略27.略 28.(同A卷第26题)29.略30.略
三. (C卷)
21.
22.
23.1 24.4x 16.
四. (C卷) 25 略26.略27.略 28.略29.(同A卷第26题)30.略