2001-2002学年第二学期教学质量检测
初一数学试卷
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 总分 |
| 得分 |
注:1、可以使用计算器,但未注明精确度的计算问题不得采取近似计算. 建议根据题型的特点把握好使用计算器的时机.
2、本试卷满分100分,在90分钟内完成. 祝你顺利并取得优秀成绩!
一、填空题:(每空2分,共30分)
1、设![]() =1,那么用含x的代数式表示y,得y=
.
=1,那么用含x的代数式表示y,得y=
.
2、如果![]() 满足方程x+ky=1,那么k的值为 .
满足方程x+ky=1,那么k的值为 .
3、若![]() ,则x+2y的值为___________.
,则x+2y的值为___________.
4、翰林汇不等式2x-7<5-2x的所有正整数解是_____________.
5、化简:① (-2002)0=______; ②(-![]() )-2 =______; ③-
)-2 =______; ③-![]() = ;
= ;
④2a3÷(-![]() a)=
; ⑤
a)=
; ⑤![]() =________.
=________.
6、“纳米(nm)”技术是一门在0.1—100纳米空间尺度内操纵原子和分子,对材料进行加工,制造出具有特定功能产品的高新技术. 纳米是一种度量单位,1纳米约为0.米,用科学记数法可将这个数表示为___________________.
7、已知点M是线段AB的中点,如果线段MB=6cm,那么线段AB= cm.
8、∠α与∠β互为余角,若∠α=15º35',则∠β等于 º ' .
9、如图,根据下列的要求,直接在下图中作图:
①利用三角板作线段CD垂直于AB,垂足为点O;
②作射线CE交线段BO于点E .
 | |||
(9) (10)
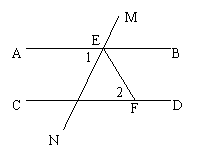
10、如图,直线AB//CD,EF平分∠BEN,若∠1=80º,则∠2=______度.
二、选择题:(每题2分,共20分,将答案直接填在下表中)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1、二元一次方程x+y=4的正整数解个数为
(A)3个 (B)4个 (C)5个 (D)无限个
2、下列不等式组中,解集为2<x<3的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3、若a<b,则下列各式中一定成立的是
(A)![]() (B)a-2>b-2 (C)-2a>-2b (D)
(B)a-2>b-2 (C)-2a>-2b (D)![]()
4、如果关于x的不等式 (m-2) x > m -2的解集是x<1,那么m的取值范围是
(A)m<2 (B)m>0 (C)m>2 (D)m>-2
5、下列计算中,结果错误的是
(A)a·a2=a3 (B)x6÷x2=x4 (C)(ab)2=ab2 (D)(-a)3= -a3
6、下列计算正确的一个是
(A)(2x +3y)(2x -3y)=2x2 -3y2 (B)(a-b)(-a+b)=a2-b2
(C)(x +y)2=x2 +y2 (D)(a + b)(a -2b) = a2 - ab-2b2
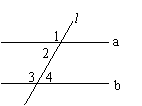
7、如图,直线a、b被直线l所截,若∠1=∠3![]() 90º,则
90º,则
 (A)∠2=∠3 (B)∠2=∠4 (C)∠1=∠4 (D)∠3=∠4
(A)∠2=∠3 (B)∠2=∠4 (C)∠1=∠4 (D)∠3=∠4
 |
(7) (8)
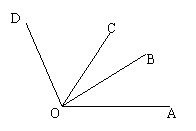
8、如图所示,∠AOD -∠AOC=
(A)∠AOC (B)∠BOC (C)∠BOD (D)∠COD
9、![]() 平角为
平角为
(A)15º (B)30º (C)45º (D)60º
10、关于同一平面内的三条直线a、b、c,有如下判断:
①若a⊥b,且a//c,则b//c; ②若a//b,且b//c,则a //c;
③若a⊥b,且b⊥c,则a⊥c; ④若a//b,且a⊥c,则b⊥c
其中正确的判断有:
(A)1个 (B)2个 (C)3个 (D)4个
三、解方程(不等式)组:(第1、2题各5分,第3题6分,共16分)
|
解:
|
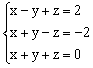
解:
|
 (要求将不等式①和②的解集在下面数轴上表示出来)
(要求将不等式①和②的解集在下面数轴上表示出来)
解:
四、计算题:(本题6分)
先化简,再求值:( -2a2b + ab2)÷( -2ab)·(a -![]() b) +
b) +![]() b2,其中a=1,b= -2
b2,其中a=1,b= -2
解:
五、阅读填空题:(每空1分,共8分)
1、如图所示,已知AO⊥OC,垂足为O,OC平分∠BOD,∠1=30° . 求∠3的度数.
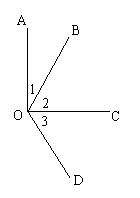 解:∵AO⊥OC (已知)
解:∵AO⊥OC (已知)
∴∠1 +∠___=90°
∵∠1=30° (已知)
∴∠2= º
又∵OC平分∠BOD (已知)
∴∠2 =∠ (角平分线定义)
∴∠3 = º (等量代换)
2、如图,已知AB∥DC,∠A=∠C,求证:∠B=∠D
 证明:∵AB∥DC (已知)
证明:∵AB∥DC (已知)
∴∠B +∠C=180° ( )
又∵∠A =∠C(已知)
∴∠B + =180° (等量代换)
∴ AD//BC ( )
∴∠C +∠D=180° (两直线平行,同旁内角互补)
∴∠B =∠D ( )
六、证明题:(本题6分)
如图,CB⊥AB,CE平分∠BCD,DE平分∠ADC,∠1+∠2=90°,求证:DA⊥AB
 证明:
证明:
七、应用题:(第1题6分,第2题8分,共14分)
1、将若干只兔放入若干个笼,若每个笼里放4只兔,则多出1只兔无笼可放;若前面每个笼放5只兔,则最后一个笼只有2只兔. 求笼的个数和兔的只数.
 解:
解:
2、中国电信开设了两种通讯业务:“全球通”,使用者每月要交月租50元和特服费6元,然后每通话1分钟,再付话费0.4元;“神州行”,不缴月租等费用,每通话1分钟,付话费0.6元(本题的通话均指市内通话). 若一个月内通话x分钟,两种方式的费用分别为y1,y2 .
①分别用含x的代数式表示出y1,y2 ;
②一个月内通话多少分钟,两种移动通讯费用一样?
③赵老师说他每月手机通话约为300分钟,请你参谋:选择那种通讯业务较合算?
解: