浙教版七年级上册同步练习7.3.1 线段的长短比较（一）
[基础训练]
1、下列图形中，可以比较长短的是 （ ）
A、两条射线 B、两条线段 C、两条直线 D、直线与射线
2、比较两条段的长短，常用的方法有 和 。
3、比较两条线段a和b的大小，结果可能有
种情况，它们是
。
4、比较下列各组线段的长短。
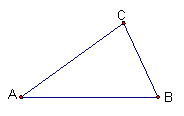5、如图，比较三角形三条边的大小，并用“<”号把它们从小到大连接起来。
6、已知线段a，利用尺规，求作一条线段AB，使AB=2a。
[综合提高]
一、选择题
1、下列说法正确的是 （ ）
A、线段、射线、直线中，直线最长
B、直线的长是射线的2倍
C、画出A、B两点间的长度
D、点C在线段AB上，则AB≧CB
2、平面上有A、B、C三点，已知AB=8cm,BC=5cm,则AC的长是 （ ）
A、13cm B、3cm C、13cm或3cm D、不能确定
二、填空题
3、如图，点C在线段AB上，
（1）AB=（ ）+（
） A
C
B
（2）AC=（ ）―（ ）
(3)若线段AB=5cm,BC=3cm,则图中最短的线段是
。
4、画直线L，并在直线L上截取线段AB=5cm，再在直线L上截取线段BC=2cm，则线段AC的长是 。
三、解答题
5、已知线段a、b，利用尺规，求作一条线段AB，使AB=a+2b
a
b
6、已知线段a、b，利用尺规，求作一条线段MN，使MN=2a-b 。
a
b
7、已知线段a和两条相交直线AB、CD（交点为O），利用尺规按下列要求画图：
（1）分别在射线OA、OB、OC、OD上作线段OA’、OB’、OC’、OD’，使它们等于线段a。
（2）顺次连结A’ 、B’、C’、D’。
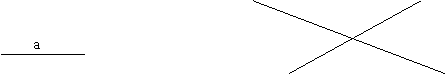（3）想一想，得到一个什么四边形？
A
C
O
D B
8、找一份地图，只用圆规，比较一下，北京、上海、西安两个城市之间的距离大小。
9、[探究创新]
如图，三角形ABC中，AB=3cm,AC=4cm,BC=5cm，用刻度尺作出每条边上的中点并顺次连它们，得到什么样的图形？量一量组成这个图形的各边的长度，并算出三角形ABC和你得到的图形的周长，发现它们之间有什么联系？再画几个三角形，重复上述过程，是否还存在你发现的规律？
A
C B
§ 7.3.2 线段的长短比较（2）
[基础训练]
1、A、B两点间的距离是指 （ ）
A、过A、B两点间的直线； B、连结A、B两点间的线段；
C、直线AB的长； D、连结A、B两点间的线段长
2、下列四个语句中正确的是 （ ）
A、如果AP=BP，那么点P是AB的中点； B、两点间的距离就是两点间的线段
C、两点之间，线段最短 D、比较线段的长短只能用度量法
3、已知A在数轴上表示的数，则与点A的距离为2个单位的点有 （ ）
A、0个 B、1个 C、2个 D、无数个
4、两点之间的所有连线中，线段 ，两点之间线段的 ，叫做这两点之间的距离。
5、如图，点M把线段AB分成相等的两条线段AM和BM，则点M叫做线段AB的 ，这时AM= AB。
A
M B
6、线段AB=6cm，延长线段AB到C，使BC=3厘米，则AC是BC的 倍。
7、已知线段AB=4厘米，延长AB到点C，使BC=1/2AB，则AC= 厘米，如果点M为AC的中点，则AM= 厘米。
8、如图,C表示一条弯曲的小河,点A、点B表示两个村庄，在何处架桥，才能使A村和B村的路程最短？说明理由。 C
· A
·B
[综合提高]
一、选择题：
1、下列说法不正确的是 （ ）
A、延长线段AB于点C，使BC=AB
B、反向延长射线OA到点B
C、点M是线段AB的中点，则AM=BM
D、若AM=BM，则点M为线段AB的中点
2、点M在线段AB上，现有四个等式（1）AM=BM （2）BM=1/2AB （3）AB=2BM （4）AM+BM=AB，其中能表示M是AB的中点的等式有 （ ）
A、1个 B、2个 C、3个 D、4个
3、如果线段AB=13厘米，MA+MB=17cm，那么下面说法正确的是 （ ）
A、M点在线段AB上 B、M点在直线AB上
C、M点在直线AB外 D、M点可能在直线AB上，也可能在直线AB外
4、长为20CM的线段AB上有一点C，那么AC、BC的中点的距离是 （ ）
A、11CM B、10CM C、9CM D、8CM
5、下列说法中正确的是 （ ）
A、延长线段AB到C，使得BC=AC B、延长线段BA到C，使得BC=AB
C、延长线段AB到C，使得BC=1/2AB D、延长线段BA到C，使得BC=1/2AB
6、下列说法正确的是 （ ）
A、线段中点到线段两个端点的距离相等 B、线段的中点可以有两个
C、到线段两个端点距离相等的点叫做线段的中点
D、乘火车从上海到北京要走1462千米，这就是说上海站与北京站之间的距离是1462米
7、己知AB=6cm，P点是到A、B两点等距离的点，则AP长为（ ）
A、3cm B、4cm C、5cm D、不能确定
8、如图，在直线AB上找出一点C，使AC=2CB，则C点应在（ ）
A、点A、B之间
B、点A的左边
C、点B的左边 D、点A、B之间或点B的右边
二、填空题
9、把一条弯曲的公路改成直道，可以缩短路程，其道理用几何知识解释应是_____________。
10、在一直道边植树6棵，若相邻两棵之间的距离均为1.5m，则首尾之间的距离为________m。
11、己知线段AB=4cm，延长AB到C，使BC=2AB，若D为AB的中点，则线段DC的长为_____________cm。
12、A、B、C是直线L上的三点，M、N分别是AB、BC的中点，如果AB=6厘米，BC=4厘米，则MN=____________厘米。
三、解答题：
13、根据下列语句画图并计算：
（1）作线段AB，在线段AB的延长线上取点C，使得BC=2AB，P是BC的中点，若AB=30厘米，求BP的长。
（2）作线段AB，在线段AB的延长线上取点C，使得BC=2AB，P是AC的中点，若AB=30厘米，求BP的长。
14、如图，B、C两点把线段AD分成2：4：3三部分，点P是AD的中点，CD=6，求线段PC的长。
探究创新
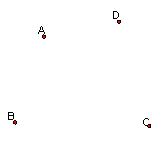
如图，平面上有A、B、C、D 4个村庄，为解决当地缺水问题，政府准备修建一个蓄水池，不考虑其他因素，请你画出确定蓄水池P的位置，使它与4个村庄的距离之和最小。
7．3．1线段的长短比较
基础训练：
1．B 2 度量法，圆规法 3.3 , a>b a=b a<b; 4. b>a , a>b, a=b, a=b 5. CB<AC<AB
6. 略
综合提高：
一．选择题：
1. D 2. D
二．填空题：
3. (1) AC, CB (2) AB, BC (3) AC; 4. 3cm 或 7cm
三．解答题：
5．略 6．略 7．略 8 上海 西安>上海 北京>西安 北京
探究创新：
9.
ABC 的周长是新三角形周长的两倍。
7．3 . 2
基础训练：
1 . B 2 .C 3 .C 4、最短，长度 ； 5.中点， 1/2； 6 .3 ； 7. 6，3 ； 8. 连接AB，两点之间，线段最短
综合提高：
一．选择题：
1 . D 2. C 3. D 4. B 5. C 6. A 7. D 8. D
二．填空题：
9．两点之间，线段最短 10. 7.5; 11. 10 12. 1cm 或 5cm
三．解答题：
13. (1)30 (2) 15; 14. 3 ;
探究创新：
连接AC ，BD 交点即为 P。