初一(下)数学期末试题
班级: 姓名: 学号:
一、填空题(第1—10题各2分,第11题6分,共26分)
1、计算 (-![]() )0= ;(-x)·(-
)0= ;(-x)·(-![]() x)= 。
x)= 。
2、已知∠α=600,那么∠α的补角等于 。
3、如果![]() 满足方程x+ky=1,那么系数k= 。
满足方程x+ky=1,那么系数k= 。
4、用科学记数法表示:0.≈ (保留两个有效数字)
5、设![]() =1,那么用x的式子表示y,得y=
。
=1,那么用x的式子表示y,得y=
。
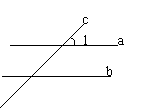
 6、如下左图,点A在直线m外,点B、C、D、在直线m上,观察图形可得点A到直线m的距离是线段
。
6、如下左图,点A在直线m外,点B、C、D、在直线m上,观察图形可得点A到直线m的距离是线段
。
7、如上右图,直线a、b被直线c所截,形成了八个角,如果a∥b,那么在这八个角中,与∠1相等的角共有 个(包括∠1在内)。
8、把(x-1)2用(x+1)2来表示,得(x-1)2=(x+1)2- 。
9、把命题“零没有倒数”改写成“如果……那么……”的形式:
如果 ,那么 。
10、已知线段AB=6cm,点M是线段AB的一个三等分点,则线段AM= 。
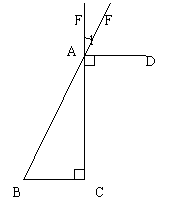 11、如图,DA⊥CE,垂足为A,BC⊥CE垂足为,∠1=35
11、如图,DA⊥CE,垂足为A,BC⊥CE垂足为,∠1=35![]() ,求∠B的度数。
,求∠B的度数。
解:∵DA⊥CE( )
∴∠DAE=900
∠DAC=900 ( )
同理∠C=900
∴∠DAC=∠C
∴AD∥BC( )
∴∠B=∠FAD( )
又∵∠1=35![]() (已知)
(已知)
∴∠FAD= . ∴∠B= 。
二、选择题(2×10=20分)
1、 下列计算正确的一个是( )
A、a6÷a3=a2 B、(a-b)(a2-ab+b2)=a3-b3 C、3-2=1/9 D、(-a)2=-a2
2、 在下列命题中的假命题是( )
A、两直线平行,内错角相等 B、两直线平行,同旁内角相等
C、同位角相等,两直线平行, D、平行于同一条直线的两直线平行
3、
方程组![]() 的解是( )
的解是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、 下列说法正确的是( )
A、延长射线OA到B B、经过两点M、N的直线有且仅有两条
C、凡是大于900 的角都是钝角 D、直线a经过点M,即是点M在直线a上。
5、 把一个不等式组的解集表示在数轴上如下左图,那么这个不等式组的整数解共有( )A、2个 B、3个 C、4个 D、无数多个
![]()
![]()
a
A B C D
-2 -1 0 1 2 3
6、 如上右图,四点A、B、C、D、都在直线a上,那么在这个图形中共有线段( )
A、3条 B、4条 C、(3+2+1)条 D、(4+3+2+1)条
7、
在3![]() 的运算中,运算依据是( )
的运算中,运算依据是( )
A、同底幂相乘的性质 B、积的乘方性质
C、幂的乘方性质 D、乘法分配律
8、
已知OC平分∠AOB,且∠AOC=22![]() ,那么∠AOB=( )
,那么∠AOB=( )
A、45![]() B、44
B、44![]() C、11
C、11![]() D、11.2
D、11.2![]()
9、
解三元一次方程组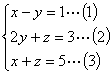 ,用加减法消去x、z的方法可以是( )
,用加减法消去x、z的方法可以是( )
A、①+②+③ B、①-②+③ C、①+②-③ D、①-②-③
10、 下面有四个同学各举了一个反例来说明命题“如果α、β都是锐角,那么
(α+β)也是锐角”是一个假命题,其中举得正确的一个反例是( )
A、 α=900, β=200 B、α=800, β=1000
C、α=400, β=300 D、α=400, β=500
三、 解答下列各题(第1、2、题各5分,第3—5题各6分,第6题2分,共30分)
1、
解不等式 ![]() ; 2、计算 (x-1)(x2+x+1)[(x+2)(x-2)+1]
; 2、计算 (x-1)(x2+x+1)[(x+2)(x-2)+1]
3、
解方程组![]()
4、
解不等式组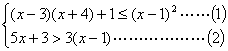
5、
先化简,再求代数式(![]() )÷(
)÷(![]() )×(a+
)×(a+![]() )+b的值,其中a=-1/3,b=1/27。
)+b的值,其中a=-1/3,b=1/27。
6、
判断方程组![]() 是否有解?为什么?
是否有解?为什么?
答: 。∵ ,∴ 。
四、何题(4+10=14分)
1、
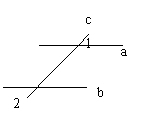 已知:如图直线a、b被直线c所截,∠1≠∠2
已知:如图直线a、b被直线c所截,∠1≠∠2
(1) a与b的位置关系是平行,还是相交?
(2)若平行,请证明;若相交,请说明交点的位置(左边或右边)
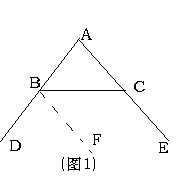
2、 填空完成证明过程:如图1,点B、C分别在直线AD、AE上,∠CBD=1350,
∠ACB=450,求证: DA⊥AE
证明方法1:过点B作BF⊥AD(过一点有且仅有一条直线与已知直线垂直)
∴∠DBF=900(垂直的定义)
 ∵∠CBD=1350(已知)
∵∠CBD=1350(已知)
∴∠CBF=
又∵∠ACB=450(已知)
∴∠ACB=∠CBF
∴AE∥BF( )
∴∠A=∠DBF( )
∴∠A=900 ∴DA⊥AE( )
证明方法2:如图2,过点A作AF∥BC( )
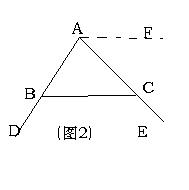 ∴∠DAF= (两直线平行,同位角相等)
∴∠DAF= (两直线平行,同位角相等)
∠CAF= (两直线平行,内错角相等)
又∵∠DBC=1350,∠ACB=450(已知)
∴∠DAF= ,∠CAF=
∴∠DAC=
∴ ( )
五、列方程组及不等式组解应用题(7+3=10分)
1、 某水果店购进苹果30箱,梨子40箱,梨子每箱进价比苹果每箱进价多5元,卖出后共获利润210元,已知苹果和梨子的利润分别是20%、25%,问苹果、梨子每箱进价各是多少元?
2、小勇身上带20元打算买3千克香蕉和3千克苹果,但到水果商店发现所带的钱不够,结果只好少买1千克香蕉,这样所带钱尚有结余,已知香蕉每1千克3元,苹果的价格也是整数,试求出苹果的价格。(只列不解)