长郡中学初一二期几何综合测试卷
姓名__________班次_________记分___________
一、判断题：（每题1分，共10分）
1．直线a外一点到a的垂线的长，叫做点到直线的距离 （ ）
2．直线外一点与直线上各点的连线中，垂线最短 （ ）
3．互为邻补角的两个角的平分线一定垂直
4．如果直线AB垂直于直线CD于O，那么Ð AOC = 90° （ ）
5．不相交的两条直线叫做平行线 （ ）
6．互补的两角一定是邻角 （ ）
7．垂线段比斜线段都短 （ ）
8．在同一平面内如果两条线段不相交，那么这两条线段就平行 （ ）
9．两条平行线被第三条直线所截，同旁内角相等 （ ）
10．两条直线被第三条直线所截，如果同位角相等，那么同旁内角互补（ ）
二、选择题（每题2分，共20分）（注：将答案填入后面的方格内）
11．点到直线的距离是指（ ）
A．从直线外一点到这条直线的垂线
B．从直线外一点到这条直线的垂线段
C．从直线外一点到这条直线的垂线的长度
D．从直线外一点到这条直线的垂线段的长度
12.平面内三条直线两两相交的交点有( )
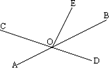A.一个 B.二个
C.三个或一个 D.四个
13．如右图，直线AB、CD相交于O，OB平分Ð EOD，
图中成对顶角的是（ ）
A．Ð AOC与ÐBOE B．ÐBOC = Ð AOD
C．ÐCOE与ÐBOD D．ÐAOE与ÐDOE
14.如右图AB、CD相交于点O，∠COE=90°，∠1=48°，则∠2、
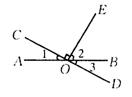∠3的大小关系是( )。
A.∠2=∠3 B.∠2＜∠3
C.∠2＞∠3 D.不能确定
15．下列各对角中，只有一条公共边并且有公共顶点的是（ ）
A．对顶角 B．内错角
C．邻补角 D．同位角
16.已知同一平面内的直线l1、l2、l3，如果l1⊥l2，l2∥l3，那么l1与l 3的位置关系是( )。
A.平行 B.相交 C.垂直 D.以上均不对
17.下列命题中的假命题是( )。
A.如果∠1和∠2是∠A的补角，那么∠1=∠2
B.如果∠3和∠4是对顶角，那么∠3=∠4
C.如果∠5和∠6是内错角，那么∠5=∠6
D.如果∠7和∠8是邻补角，那么∠7+∠8=180°
18．下列句子是假命题的为( )
A.对顶角相等 B.内错角相等
C.垂线段最短 D.两点之间线段最短
19．
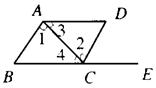如右图，点E在BC的延长线上，下列条件中不能判定
AB∥CD的是( ).
A.∠1=∠2； B.∠B=∠DCE；
C.∠3=∠4； D.∠D+∠DAB=180°
20.如果∠A和∠B的两边分别平行，那么∠A和∠B的关系是( )。
A.相等 B.互余或互补
C.互补 D.相等或互补
| 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 |
三填空题（每题2分，共10分）
21．下列四图__________________中的∠1与∠2是同位角；
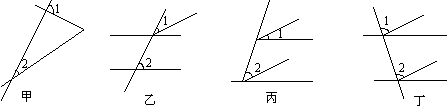
22．一个角的余角和它的补角的比是1∶ 3，此角的度数是____________;
23. 已知C是线段AB上一点，D是CB的中点，若AC = 8 cm，AB =22 cm，则线段CD=____________cm;
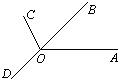
24．如图：从点O引四条射线OA、OB、OC、OD。
若
的度数之比为1∶ 2∶ 3∶ 4。
则
=_______________度。
25．命题“对顶角相等”的题设是 ，结论是 .
把“同角的余角相等”改写成“如果 ，那么 .
四、填空题：（每步2分，共30分）（注：填写推理的结果或依据）
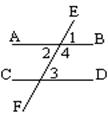
26．已知，如图：直线AB、CD被直线EF所截，
Ð 2 = Ð3，求证Ð 3 + Ð4 = 180°
证明：
∵Ð 1和Ð 2是对顶角 （ ）
∴Ð 1 = Ð 2 （ ）
∵Ð2 = Ð 3 （ ）
∴Ð 1 = Ð 3 （ ）
∵Ð 1 + Ð 4 = 180° （ ）
∴Ð3 + Ð 4 = 180° （ ）
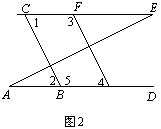27．如右图所示：填写相关的结果与理由
∵ Ð 1 = Ð 2 （已知）
∴ // （ ）
∵ Ð 3 + Ð 4 = 180° （已知）
∴ // （ ）
∵ Ð 4与Ð 5互补 （已知）
∴ // （ ）
∵ Ð A = Ð E （已知）
∴ // （ ）
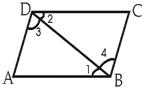28．已知：如右图，AB∥CD,∠ABC=∠ADC,
求证：AD∥BC
证明：∴AB∥CD( )
∴∠1= ( )
又∠ABC=∠ADC( )
∴∠ABC-∠1=∠ADC-∠2( )
即∠3=∠4
∴AD∥ ( )
四、解答题（每题5分，共30分）
29．线段
cm，延长线段AB到C，使BC = 10cm，再反向延长AB到D，使AD=3 cm，E是AD中点，F是CD的中点，求EF的长度。
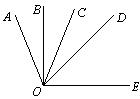
30．已知BO平分
，OB平分
，
= 90°.
，求
的度数。
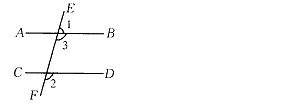31．直线AB、CD被直线EF所截，已知∠1+∠2=180°，
求证：AB∥CD。
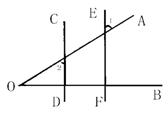32．已知，如下图，CD⊥OB,EF⊥OB,∠1=60°，求∠2的度数.
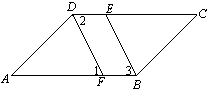33．已知Ð ABC = Ð ADC，BE、DF分别是Ð ABC、
Ð ADC的平分线，且Ð 1 = Ð 2
求证：FD // BE