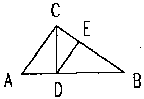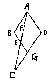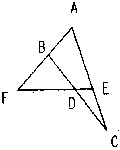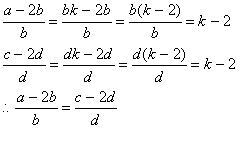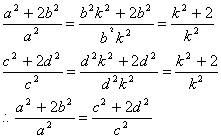初一几何线段、角、相交线、平行线练习题及答案

初一几何

一.选择题 (本大题共 32 分)

1. 如果ad=bc，那么下列比例式中错误的是（　　）
　　 　 　 　　

2. 如果 ，则下列各式中能成立的是（　　）
　　 　 　 　　

3. 下列说法中，一定正确的是（　　）
(A)有一个锐角相等的两个等腰三角形相似
(B)底角为45˚的两个等腰梯形相似
(C)任意两个菱形相似
(D)有一个钝角相等的两个等腰三角形相似

4. 延长线段AB到C,使得BC= AB,则AC:AB=(　 )
(A)2:1 　　 (B)3:1　 　 (C)3:2   　 (D)4:3

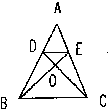
5. 如图已知：△ABC中，DE∥BC，BE、CD交于O，S_△DOE:S_△BOC=4:25，则AD:DB=（　　  ）
(A)2:5　　(B)2:3　　 (C)4:9　　 (D)3:5

6. 三角形三边之比为3:4:5，与它相似的另一个三角形的最短边为6cm，则这个三角形的周长为（　　　）
(A)12cm　　(B)18cm　  (C)24cm　　 (D)30cm

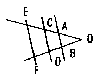
7. 如图,根据下列条件中(　 )可得AB∥EF
(A) OA:AE=OB:BF 　　 (B) AC:AE=BD:DF　 　 (C) OA:OE=OB:DF 　　 (D)AE:BF=OA:DB

8. 如图已知在Rt△ABC中，∠ACB=90˚，CD⊥AB于D，DE⊥BC于E，则图中相似（但不全等）的三角形共有（　　　）
(A)6对　　(B)8对　　 (C)9对　　 (D)10对

二.填空题 (本大题共 40 分)

1. 已知:x:y:z=3:4:5,且x+y-z=6,则:2x-3y+2z=　　　 

2. 在比例尺是1:10000的地图上，图距25mm，则实距是　　　；如果实距为500m，其图距为　　　cm。

3. 两个相似三角形对应高的比为1:√2，则它们的周长之比为　　　；面积之比为　　　。

4. 如果△ABC∽△ADE，且∠C=∠AED，那么它们的对应边的比例式为　　　　　  。

5. 两个相似多边形面积之比为3:4，则它们的相似比为　　　。

6. 已知 ,则

7. 如果 ，则 ， 。

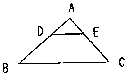
8. 如图已知:△ABC中,DE∥BC, 　,则 , 。

9. 线段AB=15cm，C在AB的延长线上，且AC:BC=3:1，则：BC=　　  cm。

10. 顺次连结三角形三边中点所成的三角形面积与原三角形面积之比为　　　 。

三.解答题 (本大题共 8 分)

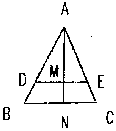
1. 如图已知:△ABC中,DE∥BC,DE=8,BC=12,AN⊥BC交DE于M,四边形BCED的面积为90。
求:△ADE的面积及AM、AN的长。

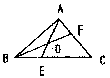
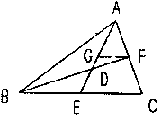
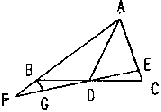
2. 如图已知:△ABC中,F分AC为1:2两部分,D为BF中点,AD的延长线交BC于E.求:BE:EC

四.证明题 (本大题共 20 分)

1. 已知：
求证:（1）
　　　　（2）

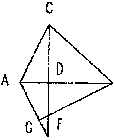
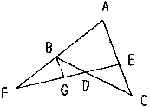
2. 如图已知:菱形ABCD中，E为BC边上一点，AE交BD于F，交DC的延长线于G。
　　求证:

3. △ABC中，D为BC中点，过D的直线交AC于E，交AB的延长线于F。　 
 求证:

4. △ABC中,D为BC中点,过D的直线交AC于E，交BA的延长线于F.
求证:  

5. 如图已知:CD是Rt△ABC的斜边AB上的高，E为CD延长线上一点，连接AE，过B作BG⊥AE于G，交CE于F。
求:△ADE的面积及AM、AN的长。

初一几何 —— 答案

一.选择题 (本大题共 32 分)

1. ：C

2. ：C

3. ：D

4. ：C

5. ：B

6. ：C

7. ：A

8. ：C

二.填空题 (本大题共 40 分)

1. ：8

2. ：250m，5

3. ：1:√2，1:2

4. ：

5. ：√3:2

6. ：

7. ：

8. ：

9. ：7.5

10. ：1:4,

三.解答题 (本大题共 8 分)

1. ：解:DE∥BC，△ADE∽△ABC
　　　　　
　　　　　 S_△ADE=x，S_△ABC=x+90
　　　　　 　 x=72　　S_△ADE=72

　　　　　　 DE•AM=72　　　　 AM=12

　　　　　 　　 　　 AN=18
　　　　　 答:△ADE的面积为72，AM=12，AN=18

2. ：解:过F作FG∥BE交AD于G,则:∠GFD=∠EBD
　　　　　 FG/EC=AF/AC=1/3
　　　　　 在△BED和△FGD中,
　　　　　  ∠EBD=∠FGD
　　　　　　　 BD=FD
　　　　　　　 ∠BDE=∠FDG
　　　　　 △BED≌△FGD(ASA)
　　　　　 BE=FG
　　　　　 BE/EC=AF/AC=1/3

四.证明题 (本大题共 20 分)

1. ：证明:设： 则：a=bk，c=dk
　　　　　　 （1）

　　　　　　 （2）
 

2. ：证明:BE∥AD，　　 　 ∴

　　　　　　　　　　　　  又∵AB∥DG，　 ∴
　　　　　　　　　　　　  而AB=AD，　　　　 ∴
　　　　　　　　　　　　  即:　

3. ：证明:过B作BG∥AC交DF于G，则:
　　　　　　 ∠GBD=∠C
　　　　　　 在△GBD和△ECD中
　　　　　　  ∠GBD=∠C
　　　　　　  ∠BDG=∠CDE
　　　　　　  BD=CD
　　　　　　 ∴△GBD≌△ECD （AAS）
　　　　　　 ∴BG=EC，　　
　　　 ∴

4. ：证明:过B作BG∥AC,
　　　　　　 则: 　 ∠GBD=∠C
　　　　　　 在△GBD和△ECD中,
　　　　　　  ∠GBD=∠C(已证）
　　　　　　　  BD=CD　（中点性质）
　　　　　　  　∠BDG=∠CDE（对顶角）
　　　　　　 ∴△GBD≌△ECD(ASA)
　　　　　　 ∴BG=EC
　　　　　　 ∴ 　

5. ：证明:在Rt△ABC中,CD⊥AB
　　　　　　 ∴△ADC ∽△CDB,　　　　　∴　  　　　 即CD²=AD•BD
　　　　　　 ∵∠E+∠EAD=90˚,　 ∠ABG+∠EAD=90˚ 
　　　　　　 ∴∠E=∠ABG,　　  即:∠E=∠DBF
　　　　　　 ∴Rt△AED ∽Rt△FBD
　　　　　　 ∴ ,即:ED•FD=AD•BD
　　　　　　 ∴CD²=ED•FD