初一（下）综合练习
班级： 姓名： 学号：
一、填空题（第1—11题各2分，12、13题各6分共34分）
1、
计算：(
)º ,
= .
2、
如右图，点C在直线AB上，那么以A、B、C为端点的线段共有 条，以A、B、C为端点的射线共有 条。
3、 设t=x-1，那么用t的式子表示x，得x= 。
4、
计算 -
=
。
5、 已知点M是线段AB的中点，如果线段MB=6cm，那么线段AB= 。
6、
不等式
的解集是
。
7、
已知∠
，那么∠α的余角等于
。
8、
化简 2a3÷(-a)=
.
9、 经过一个点有 条直线；经过两个点有且 条直线。
10、 已知a+b=5，ab=6，那么计算(x+a)(x+b)= 。
11、 把命题“钝角的一半是锐角”改写成“如果……那么……”的形式：
如果 ，那么 。
12、
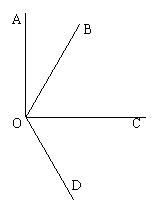如图，已知AO⊥OC，垂足为O，OC平分∠BOD，∠1=30º。
求：∠COD的大小。
解：∵AO⊥OC ( )
∴∠1+∠2=90º ( )
∵ （已知）
∴∠2=60º
又OC平分∠BCD（已知）
∴∠3= （ ）
即∠COD= 。
13、
解方程组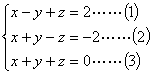
解：由① ②，解得x= ；由③ ①，解得y= ；
把求得的x、y的值代入③，解得z= ，∴原方程组的解是 。
二、选择题 （2×10=20分）
1、
平角=（ ）A、150 B、300 C、450 D、600
2、用科学记数法表示0.，保留2个有效数字，得（ ）
A、7.0×104
B、7.0×10-4 C、7.03×104
D、7.03×10-4
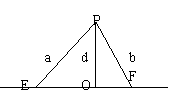
3、如图，PO⊥EF，垂足为O，线段OE>OF，
线段PO=d，点P到点E、F、的距离分别为a、b，
那么d、a、b的大小关系是（ ）
A、a>b>d B、a>d>b C、b>a>d D、d>b>a
4、计算 2x2y·3xy2=2×3·x2·x·y·y2=6x3y3，在这个计算过程中，先后用到的运算律是（ ）
A、乘法交换律，乘法结合律 B、乘法结合律，乘法分配律
C、乘法交换律，乘法分配律 D、乘法结合律，乘法交换律
5、∠α的补角等于（ ）
A、1800-∠α B、1800+∠α C、900-∠α D、900+∠α
6、如果∠1与∠2是内错角，∠2与∠3是同旁内角，那么∠1与∠3的位置关系只能是（ ）A、对顶角 B、同位角 C、对顶角或同位角 D、邻补角
7、在数对①
，②
，③
中，满足方程3x-2y=3的是（ ）
A、①② B、②③ C、①③ D、①②③
8、下列计算不正确的一个是（ ）
A、a2 •a3=a5 B、x6÷x2=x4 C、(x-y)2=x2-y2 D、(2a)3=8a3
9、下列说法正确的一个是（ ）
A、两条射线组成的图形叫做角 B、连结两点的线段叫做这两点间的距离
C、射线AB与射线BA是同一条射线
D、两条直线被第三条直线所截，同位角不一定相等
10、给出以下四个推理：
① 如果直线a、b、c中，a⊥b，b⊥c，那么a⊥c。
② 如果直线a、b、c中，a∥b，b∥c，那么a∥c。
③ 如果三个数a、b、c中，a>b，b>c，那么a>c。
④ 如果三个数a、b、c中，a≥0，b<c，那么ab<ac。
其中，推理正确的是（ ）A、①②③ B、②③④ C、②③ D、②④
三、解答下列各题（1—3题各5分，4、5题各6分，共27分）写出解答过程
1、 解不等式 (x+1)2<(x+1)(x-1)+8
2、
计算 [(x-y)(x2+xy+y2)-4y2(x-
y)]÷x
3、 计算 x3y(y3-3y2+9y-27)(y+3)
4、
用代入法解方程组
5、
解不等式组
（要求：把数轴上表示不等式组解集的图形保留在试卷上）
四、何题（5+7=12分）
1、如图，在射线OB上截取OC=6cm，过点C作CD⊥OA，垂足为D，由此量得∠OCD= ，量得点C到OA的距离为 =
cm
2、如图，已知AB∥DC，∠A=∠C求证：∠B=∠D
证明：∵AB∥DC（已知）
∴∠B+ =1800（两直线平行，同旁内角互补）
又∵∠A=∠C（已知）
∴∠B+ =1800（等量代换）
∴ （同旁内角互补，两直线平行）
∴∠C+ =1800（ ）
∴ （ ）
五、列方程组解应用题（7分）
1、A市与B市相距18km，甲、乙二人骑自行车分别从两市区同时出发，相向而行，行了36分钟两人相遇，若行1小时，甲所余路程是乙所余路程的2倍。甲、乙二人（每小时）的平均速度各是多少？
2、某服装店以进价30元购进80件衬衫，若按原订售价可以全部售完，则可获得的利润不低于600无际；若按每件增加5元，就会有1/3的衬衫卖不出去，这样获得的利润不会超过400元，原订售价每件大约多少元？（只列不解）