第五章 二元一次方程
本章主要内容：二元一次方程及其解集。方程组和它的解，解方程组。用代入（消元）法、加减（消元）法解二元一次方程组。三元一次方程组及其解法举例。一次方程组的应用。
5.1 二元一次方程组
【学会归纳】
1. 叫二元一次方程，
例如方程 是一个二元一次方程。
2. 叫二元一次方程组，
例如方程 是一个二元一次方程组。
3. 叫做二元一次方程组的解，
例如 是方程组 的解。
【学会探究】
问题1 下列方程中，是二元一次方程的是（ ）
（A）
（B）
（C）
（D）
问题2 下列方程组中，是二元一次方程组的是（ ）
（A）
（B）
（C）
（D）
问题3 方程组
的解是（ ）
（A）
（B）
（C）
（D）
要弄懂二元一次方程、二元一次方程组和它的解的含义，并会检验一对数是不是某个二元一次方程组的解。
注意二元一次方程的条件：
（1）二个未知数
（2）未知项的次数是1
（3）必须是整式方程
作为二元一次方程组的两个方程，不一定都是含有两个未知数。
使方程组中的每个方程的两边都相等的未知数的值才是方程组的解
问题4 已知
是关于
、
的方程
的一个解，求
的值.
问题5 二元一次方程
的正整数解分别有哪几个?
【学会实践】
1.若方程
是关于、的二元一次方程,则
2.已知
是关于、的二元一次方程
的一个解,则
.
3.方程
有______个解,其中_______是其中的一个.
本题考察对二元一次方程的解的理解,方法是把、的值代入方程可得关于的一元一次方程.
本题有助于加深对二元一次方程的解的理解和掌握.注意
是偶数,则是小于5的奇数,用实验法就可正确解出.
注意二元一次方程的定义.
4.在方程组
、
、
、
、
中属于二元一次方程组的有________个.
5.解是
的二元一次方程组是( )
(A)
(B)
(C)
(D)
6.
是方程组
的解,则( )
(A)
(B) 
(C) 
(D) 
、
的值不能确定
7.要把一张面值为10元的人民币换成零钱,现有足够的面值为2元、1元的人民币,那么共有换法( )
(A)5种 (B)6种 (C)8种 (D)10种
可设元列出二元一次方程,分析方程的解的特点.
【学会自检】
学会探究答案:
1.(C)
2.(B)
3.(D)
4.3
5.
学会实践答案:
1.
2.
3.无数个解,任填一个解
4.1个
5.(C)
6.(B)
7.(B)
5．2 用代入法解二元一次方程组
【学会归纳】
用代入法解二元一次方程组的一般步骤：
1．把一个方程里的一个未知数，用含有 表示出来，在选元时，必须注意计算简便；
2．把这个代数式代入 而消去一个未知数，得到一个一元一次方程；
3．解这个一元一次方程，求出一个未知数的值；
4．把求得的这个未知数的值代入第一步所得的代数式中，求出另一个未知数的值；
5．把这两个未知数的值用
的形式写在一起，以表示方程组的解。
【学会探究】
问题1 用代入法解方程组
问题2 用代入法解方程组
把方程（1）代入方程（2）就可把原二元一次方程组化为一元一次方程组
通常，当某个未知数的系数的绝对值为1时，将它所在的方程变形
问题3 用代入法解方程组
问题4 用代入法解方程组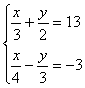
问题5 用代入法解关于、方程组
代入法消元法的通常是，把方程组中的某个方程的一个未知数（系数最为简单的）用另一个未知数的代数式来表示
应先把分数系数化为整数系数，即把原方程组化简。
解字母系数的二元一次方程组与上述解问题的方法是一致的
【学会实践】
1．用代入法解方程组：
2．用代入法解方程组：
3．用代入法解方程组：
当你看到方程组中有一个方程是关于“一个未知数用含有另一个未知数的代数式来表示”时，就把它代入另一个方程吧
你看，方程组中的第一个方程中，含的项的系数多么简单，该知道如何解决了吧
想消去哪个未知数？告诉你一个今人振奋的方法：由第一个方程得
，把它代入第二个方程，你试过这种方法吗？这叫整体代入法
4．用代入法解方程组：
【学会自检】
学会探究答案：
1.
2．
3．
4．
5．
先化简吧，它能使你的解题更简洁
学会实践答案：
1.
2. 
3.
4.
5．3 用加减法解二元一次方程组
【学会归纳】
用加减法解二元一次方程组的一般步骤：
1．使方程组中的某个未知数的系数的 相等。
2．把两个方程两边分别 或 ，消去一个未知数，得到一个一元一次方程。
3．解这个一元一次方程。
4．将求出的未知数的值代入原方程组中的任意一个方程中，求出另一个未知数的值，从而求得方程组的解。
【学会探究】
问题1 用加减法解方程组：
问题2 用加减法解方程组：
本问题可用加法求出的值，用减法用求的值
有相同系数的未知数该“倒霉”了
问题3 用加减法解方程组：
问题4 用加减法解方程组：
问题5 用加减法解方程组：
要想消去某个未知数，就请主它们的系数的绝对值相等吧
还是先考虑代简吧
【学会实践】
1．用加减法解方程组：
2．用加减法解方程组：
3．用加减法解方程组：
4．用加减法解方程组：
5．用加减法解方程组：
6．用加减法解方程组：
【学会自检】
学会探究答案：
1.
2.
3.
4.
5.
学会实践答案：
1.
2.
3.
4.
5.
6.
5．4 三元一次方程组的解法
【学会归纳】
方程组有 个未知数，每个方程的未知项的次数都是 次，并且一共有 个方程，这样的方程组是三元一次方程组；解三元一次方程组的指导思想是“ ”，利用代入法或加减法消去一个或两个未知数，把三元一次方程组化成二元一次方程组或一元一次方程，注意在消元的过程中每个方程至少用一次。
【学会探究】
问题1 解方程组
问题2 
在这个方程组中，方程（1）只含有两个未知数、
，所以只要由（2）（3）消去
，一就可以得到只含有、的二元一次方程组
用加减法解时，应选择消去系数绝对值最小的最小公倍数的最小的未知数
问题3 解方程组
【学会实践】
1．
2．
还记得吗？题中的
就是
3．
【学会自检】
学会探究答案：
1.
2.
3.
学会实践答案：
1.
2.
3.
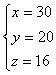
5．5 一次方程的应用
【学会归纳】
运用一次方程组解应用题的步骤是（1）审题（2）设未知数，找等量关系（3）列方程组（4）解方程组（5）检验并写出答案
【学会探究】
问题1 甲、乙两个人相距 20km，甲骑自行车，乙步
行，二人同时出发，相同而行，甲5小时可追上乙；相向而行2小时相遇，二人平均速度各是多少？
问题2 李明以两种形式分别储蓄了2000元和1000元，一年后全部取出，扣除利息所得税后可得利息43.92元.已知这两种储蓄利率的和为3.24%，问这两种储蓄的年利率各是百分之几？
（注：公民应交利息所得税=利息金额×20%）
问题3 八十年代，A市改革开放的十年，工农业总产值由175亿元上升到423亿元，其中工业产值是十年前的2.7倍，农业产值是十年前的1.8倍.求十年前A市的工业、农业产值各为多少亿元？
不能用已知量（路程20km）和设元（速度）作等量关系，只能用时间作等量关系，找出两句关于时间的句子，那可是列两个方程的依据
纳税可是每人公民应
尽的光荣义务
问题4 要配制浓度是6%的某种药液700克，已有浓度为5%的这种药液200克，还需要再加入浓度是8%的药液和水各多少克？
问题5 有一个两位数，个位上的数字比十位上的数字大5，如果把这两个数字的位置对换，那么所得的新数与原数的和是143，求这个两位数.
【学会实践】
1. 据《新华日报》消息，巴西医生马廷恩经过10年研究后得出结论，卷入腐败行为的人容易得癌症、心血管病。如果将犯有贪污、受贿罪的580名官员与600名廉洁官员进行比较，可发现，后者的健康人数比前者的健康人数多272人，两者患病（包括致死）者共444人。试问：犯有贪污、受贿罪的官员的健康人数占580名官员的百分之几？廉洁官员的健康人数占600名官员的百分之几？
2．已知甲．乙两种商品的原单价和为100元，因市场变化，甲商品降价 10％，乙商品提价 5％，调价后，甲、乙两种商品的单价和比原单价和提高了 2％，求甲．乙两种商品的原单价各是多少元？
3．某工厂在规定天数内生产一批抽水机支援抗
旱，如果每天生产25台，那么差50台不能完成任务；如果每天生产28台，那么可以超额40台完成任务，问这批抽水机有多少台？规定几天完成任务？
4．把含盐40%的食盐水和含盐15%的食盐水混合制成含盐25%的食盐水5公斤，应取这两种食盐水各多少公斤？
【学会自检】
学会探究答案：
1. 甲速7千米/小时、乙速3千米/小时
2. 2.25％、0.99％
3. 工业产值为120亿元
农业产值为55亿元
4. 400克、100克
5. 49
学会实践答案：
1. 49％、84％
2. 20元、80元
3. 800台、20天
4. 2公斤、3公斤