初一数学第二学期周练（五）
（垂线、平行公理）
一、判断：（
）
1、如果一对对顶角互为补角，则构成这两个角的两条直线互相垂直。 （ ）
2、连结直线外一点与直线上任意一点的线段的长度叫点到直线的距离。 （ ）
3、过一点作已知直线的平行线有且只有一条。 （ ）
4、不相交的两条直线叫平行线。 （ ）
5、若直线
∥
，∥
，∥
，则∥。
（ ）
二、填空：（
）
1、按要求画图（用三角板和铅笔）并填空：
在图（1）中，过P点作AB的垂线_____________，过P点作CD的垂线_____________。
在图（2）中，过A点作BC的垂线段_____________，过C点作AB的垂线段_____________。
在图（3）中，过A点作DC的垂线段_____________，过D点作BC的垂线段_____________。
在图（4）中，分别过三角形三个顶点作对边所在直线的垂线，则三条垂线段分别为_____________、_____________、_____________。
2、如图，P是直线外一点，过P作的垂线段PA，再在上作两点B、C，分别满足∠PBA=45°，∠PCA=30°，则量出：P到的距离是_____________（cm），线段AB=_____________（cm），线段PC=_____________（cm）；则P到的距离与线段AB的长度关系是_____________，线段PA与PC的长度关系是_____________。
3、平面内共有10条直线，则其交点的个数最少有_____________个，最多有_____________个，若其中有4条直线两两平行，则这10条直线交点的个数为_____________个。
三、选择题：（
）
1、平面内两条直线的位置关系可能是（ ）
（A）相交或垂直或平行 （B）相交或平行或异面
（C）相交或平行 （D）垂直或平行
2、点到直线的距离是指这点到这条直线的（ ）
（A）垂线 （B）垂线段 （C）垂线的长度 （D）垂线段的长度
3、直线、、、
在同一平面内，已知∥，∥，且直线与相交于P点，则与一定（ ）
（A）平行 （B）相交 （C）异面 （D）无法确定
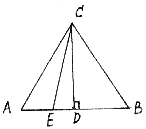
4、如图，P是AB中点，CD⊥AB，则下列说法正确的个数有（ ）
① 线段AB是CD的垂直平分线。
② CD上任意一点到A、B两点的距离相等。
③ C点到A点的距离大于C点到直线AB的距离。
④ 三角形ABC的面积
。
（A）4 （B）3 （C）2 （D）1
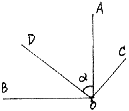
5、如图，已知AO⊥BO，DO⊥CO，∠AOD=
，则∠BOC的度数为（ ）
（A）
（B）
（C）
（D）
6、已知OA⊥OC，∠AOB:∠AOC=1:3，则∠BOC的度数是（ ）
（A）60° （B）120° （C）60°或120° （D）以上答案都不对
四、解答题：（
）
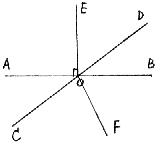
1、如图，已知直线AB、CD相交于O，OE⊥AB，OF平分∠COB，∠AOC=32°，求∠EOF的度数。（有过程，注理由）
2、已知线段AB被分成2:3:4三部分，且第一部分与第三部分的中点的距离为4.8cm，求AB的长。
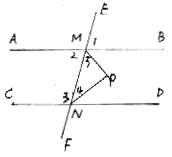
3、如图，已知AB、CD与直线MN交于M、N两点，∠1=∠MND，MP、NP分别平分∠BMN和∠MND，求证：① ∠2与∠3互补；② ∠5+∠4=90°。（注理由）
4、已知在同一平面内三条直线、、满足∥，∥，求证：∥。
参考答案：
一、判断：（5×2′=10′）
1．√ 2．× 3．× 4．× 5．√
二、填空：（17×2′=34′）
1．
2．1.1 1.1 2.2 相等 PC=2PA
3．0 45 39
三、选择题：（6×3′=18′）
1．C 2．D 3．B 4．B 5．A 6．C
四、解答题：（2×9′+2×10′=38′）
1．∠EOF=164°
2．AB=7.2cm
3．证明：∵∠1=∠MND（已知）
∠1=∠2（对顶角相等）
∴∠2=∠END（等量代换）
∵∠3+∠END=180°（邻补角）
∴∠2+∠3=180°（等量代换）
即∠2与∠3互补
∵∠1=∠MND
又∵∠1+∠BMN=180°
∴∠MND+∠BMN=180°（等量代换）
∵MP平分∠BMN
∴
同理
∴
=90°
即∠5+∠4=90°
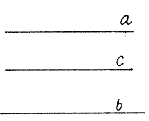
4．证明：假设a与c相交，设交点为P
则：∵a∥b，c∥b
∴过点P有两条直线都与b平行，这与平行公理过直线外一点有且只有一条直线与已知直线平行矛盾。
∴假设不成立
∵a、c在同一平面内
∴a∥c