圆复习测试
班级________学号_________姓名_________________
一、填空(每题2分,共30分)
1、在⊙O中，AB是直径，CD是弦，若AB⊥CD于E，且AE=2，BE=8，则CD=______.
2、在圆内接四边形ABCD中，若AB=BC=CD，AC是对角线，∠ACD=30°，则∠CAD=______°.
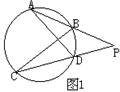
3、如图1,∠APC=30°，弧BD等于30°，则弧AC等于_______°,∠AEB=_____°.
4、过⊙O内一点P，的最长弦是10，最短的弦是6，那么OP的长为____________.
5、圆内相交的两弦中，一弦长是20，且被交点平分，另一弦被交点分成两线段之比是1：4，另一弦长是____________.
6、在圆内接四边形ABCD中，∠A：∠B：∠C=5：2：1，则∠D=_______.
7、若PA、PB分别切⊙O于A、B，∠APB=60°，OP=12，则OA=______,PB=________.
 |  |  | |||
8、⊙O的内接正方形ABCD的边长为6，E是BC的中点,AE的延长线交⊙O于F，则EF=______
 |
9、△ABC中,∠A=80°,若O1是内心,则∠BO1C=_____；若O2是外心,则∠BO2C=______.
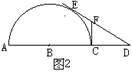
10、如图2，AB=BC=CD，过点D作B的切线DE，E为切点，过C点作AD的垂线交DE于F，则EF：FD=___________(填比值).
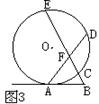
11、如图3，⊙O中弦AD、CE相交于点F，过点A作⊙O的切线与EC延长线相交于点B，若AB=BF=FD，BC=1，CE=8，则AF=______________.
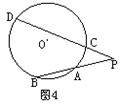
12、如图4，PAB、PCD是⊙O的两条割线。且PA=AB，CD=3PC，则PC：PA=______.
二、选择题（每题3分，共27分）
1、下列命题中假命题是 （ ）
A．相等的圆心角所对的弧相等 B．圆内接四边形对角互补
C．一条弧的对的圆心角等于它所对的圆周角的2倍 D．直径所对的圆周角是直角
2、圆的外切平行四边形为 （ ）
A．矩形 B．菱形 C．等腰梯形 D．平行四边形
3、已知⊙O的半径为6cm,⊙O的一条弦AB的长为
cm,则弦AB所对的圆周角是
（ ）
A．30° B．60° C．30°或150° D．60°或120°
4、若两半径分别是R和r,圆心距是d,且
,则两圆位置关系是（ ）
A．外切或内切 B．外离 C．相交 D．内含
5、已知两圆的半径分别是方程
的两根，圆心距为12，那么两圆公切线的条数是
（ ）
A．1 B．2 C．3 D．4
6、半径为为25cm的⊙O中，弦AB=40cm，则此弦和所的对弧的中点的距离是（ ）
A．10cm B．15cm C．40cm D．10cm和40cm
7、圆心在
轴上的两圆相交于A、B两点,A点的坐标为
，则B点的坐标是（ ）
A．
B．
C．
D．
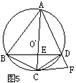8、如图5，ABCD为⊙O的内接四边形,AC平分∠BAD,并与BD交于E点，，CF切⊙O于C点并与AD的延长线交于F，图中的四个三角形：①△CAF；②△ABC；③△ABD；④△BEC，其中与△CDF一定相似的是 （ ）
A．①②③ B．②③④ C．①③④ D．①②④
9、以长为a的线段AB为斜边的Rt△ABC的直角顶点C的轨迹是（ ）
A．与AB平行且到AB距离为
的一条直线；
B．与AB平行且到AB距离为的二条直线；
C．以AB的中点为圆心，为半径的一个圆；
D．以AB为直径的一个圆（A、B两点除外）。
三、计算题（18分）
1、已知：⊙O的外切等腰梯形的中位线长为10，两底长的差为12，求⊙O的半径。
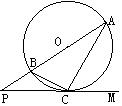
2、如图，AB是⊙O的直径，PCM与⊙O相切于点C，且∠ACM=57°,求P的度数。
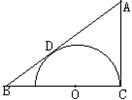
3、如图，△ABC中，∠C=90°，点O在BC边上，半圆O过点C，切AB于点D，交BC于E，又BE=1，BD=2，求AD的长。
三、证明题（25分）
1、如图，已知：AB是⊙O的直径，BC是⊙O的切线，切点为B，OC∥弦AD。
求证：DC是⊙O的切线。
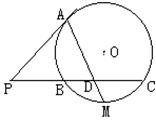2、如图：PA切⊙O于点A，PBC交⊙O于点B、C，M是弧BC的中点，AM交BC于点D。求证：
3、如图，已知：ADB、AEC是⊙O的两条割线，PA∥ED交CB的延长线于点P，PE切⊙O于点F。
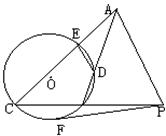求证：PA=PF。
附加题
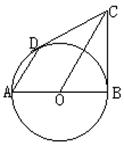
已知：如图，在△ABC中，AB=AC，以AB为直径作圆分别交BC、AC于D、G，作DE⊥AC于E，连结BE交⊙O于F。
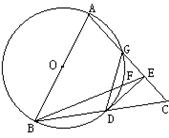求证：（1）DE为⊙O的切线；
（2）DG=DC；
（3）AE·EC=BE·EF