二十 分数问题(一)
年级 班 姓名 得分
一、填空题
1．分数
、
、
、
从小到大排列为 .
2.有分母都是7的真分数、假分数和带分数各一个，它们的大小只差一个分数单位.这三个分数分别是 .
3.已知
A、B、C、D四个数中最大的是 .
4.所有分子为11,而且不能化成有限小数的假分数共有 个.
5.在等式
中,a,b都是由三个数字1,4,7组成的带分数,这两个带分数的和是 .
6.在下面算式的两个括号中,各填入一个三位数,使等式成立:
.
7.将五个数
按从小到大的顺序排列,其中第3个位置与第4个位置上的两数之和为 .
8.设
化为循环小数后,它们的循环节长度分别是m,n,k(即它们的循环节分别有m,n,k位),则m+n+k= .
9.把
表示成三个不同的分数单位和的式子是 .
10.小林写了八个分数,已知其中的五个分数是
、
、
、
、
，如果这八个分数从小到大排列的第四个分数是，那么按从大到小排列的第三个分数是 .
11．如果
，其中A>B,求A¸B.
12.将
写成分母是连续自然数的五个真分数的和.
13.在分母小于15的最简分数中,比
大并且最接近的是哪一个?
14.分数
中的a是一个自然数,为了使这个分数成为可约分数, a最小是多少?
———————————————答 案——————————————————————
1.
、
、
、.
2.
，
，
.
3. B.
从题目看,A、B、C、D中最大的,即为
与
与15.2¸
与14.8´
中最小的,容易求出,与B相乘的最小,所以B最大.
4. 4.
符合题意的假分数有
、
、
和
共4个.
5. 
.
由1,4,7三个数字组成的带分数有
,
,
,经验算,只有a=,b=符合条件.a+b=.
6．
.(填出一组即可)
提示:设a,b为1998的两个互质的约数,且a>b.将
分解为两个单位分数之差,得到
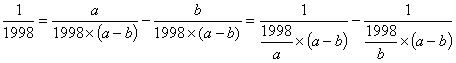.因为
与
都是三位数，所以100
.100
,得
所以
.
又由
,得
,
,所以
,
.由此得到:
①
也就是说,只要找到满足①式的1998的两个(互质的)约数,就能得到符合题意的一组解.满①式的a,b有三组:3，2；54，37；37，27.于是得到
7. 
.
通过通分(找最简公分子),
.显然
,因此,
.所求两数之和为
.
8. 14.
,
,
.
故m=3,n=6,k=5,因此m+n+k=14.
9. 
.
.
10. .
提示:已知的五个分数从大到小排列依次为、、、、，因此未知的三个分数都小于.
11. 注意到1997是质数,其约数为1和1997.
.
所以A=1997´1998,B=1998.故A¸B=1997.
12. 原式=
=
+
=
13. 设所求的分数为
,(m,n)=1,n<15.
因为-=
.
由题目要求,取m、n使右边式子大于0,且为最小,若5m-2n=1,则m=
当n<15时,使m为整数的最大整数n是12,此时,m=5,差为
.
若5m-2n¹1,则
.故此大并且最接近的是
.
14. 
.
原分数是可约分数,
也应是可约分数,推知a最小是11.