2002——2003年度第二学期期中考试七年级数学试卷
（满分120分，时间120分钟）
一、选择题（每小题3分，共36分）
1、对于下列式子①ab；② ；③ ；④ ；⑤ ，以下判断正确的是（ ）
A、①③是单项式 B、②是二次三项式 C、①⑤是整式 D、②④是多项
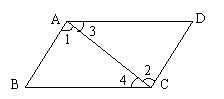
2、如图，由∠1=∠2，则可得出（ ）
A、AD∥BC B、AB∥CD
C、AD∥BC且AB∥CD D、∠3=∠4
3 下列各式的计算中，正确的是（ ）
A、
B、
C、
D、
4、对于四舍五入得到的近似数3.20×105，下列说法正确的是（ ）
A、有3个有效数字，精确到百分位 B、有6个有效数字，精确到个位
C、有2个有效数字，精确到万位 D、有3个有效数字，精确到千位
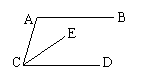5、已知：如图AB∥CD，CE平分∠ACD，∠A=110°，则∠ECD等于（ ）
A、110° B、70° C、55° D、35°
6、如果 ，那么 的值是（ ）
A、2 B、4 C、0 D、－4
7、下列各题的数，是准确数的是（ ）
A、初一年级有800名同学 B、月球离地球的距离为38万千米
C、小明同学身高148cm D、今天气温估计28℃
8、一幅扑克去掉大小王后，从中任抽一张是红桃的概率是（ ）
A、 B、 C、 D、
9、m、n为自然数，多项式
的次数是（ ）
A、m B、n C、m，n中较大的数 D、m+n
10、1纳米相当于1根头发丝直径的六万分之一。则利用科学记数法来表示，头发丝的半径是（ ）
A、6万纳米 B、6×104纳米
C、3×10－6米 D、3×10－5米
11、已知，
，
，那么xy的值是（ ）
A、－2 B、2 C、－3 D、3
12、下列说法中正确的有几个（ ）
（1）“每次摸一个球，摸到红球的概率是 ”，就是指按要求摸6次，必有一次摸到的是红球。
（2）在公式 （a≠0）中，p不能为负数；
（3）在等式
中，当x无论取什么值时都成立；
（4）概率的大小是指一事件发生的可能性大小，所以仍然不能确定该事件是否一定发生，所以学习概率对生活实际没什么帮助。
A、1个 B、2个 C、3个 D、4个
二、填空（每小题4，共16分）
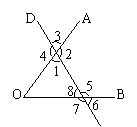
1、如图，在直线DE与∠O的两边相交，
则∠O的同位角是 。
∠8的内错角是 。
|
∠1的同旁内角是 。
2、单项式 的系数是
3、小颖看小明是北偏东30°，那么小明看小颖时，它的方向是
4、∠1与∠2互余，∠2与∠3互补，∠1=63°，那么∠3=
三、解答题
1、计算题：
（1）（2x+y）（x－y） （5分） （2）（a+b－3）（a－b+3）（要求用乘法公式6分）
（3）先化简再求值（7分）
，其中x=10，y=
2、如图，已知：∠AOB=138°（6分）
∠AOC=∠BOD=90°，求∠COD的大小
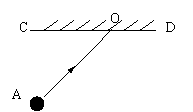
3、（4分）如图：打台球时，小球由A点出发撞击到台球桌边CD的点O处，请用尺规作图的方法作出小球反弹后的运动方向（不写作法，但要保留作用痕迹）
 |
4、（8分）一个小妹妹将10盒蔬菜的标签全部撕掉了。现在每一个盒子看上去都一样，但是她知道有三盒玉米、两盒菠菜、四盒豆角、一盒土豆，她随机地拿出一盒打开它。求（1）盒子里是玉米的概率是多少？（2）盒子里面是豆角的概率是多少？（3）盒子里删去不是菠菜的概率是多少？（4）盒子里是豆角或土豆的概率是多少？
5、（8分）一个长方形的周长是4a－8b－4c，它是长是a－2b－c 。（1）求它的宽是多少？（2）求它的面积是多少？
6、（8分）已知：如图∠1=∠2，当DE与FH有什么位置关系时，CD∥FG？并说明理由
 |
7、（5分）“非典”是由一种冠状病毒引起的非典型肺炎，具有极强的危害性及传染性，已引起了国务院及世界卫生组的关注。下表是2003年4月23日全国内地部分省市“非典”疫情：
| 省（市）区 | 广东 | 北京 | 山西 | 内蒙古 | 广西 | 四川 |
| 病例（人） | 1344 | 693 | 457 | 36 | 15 | 8 |
（1）请根据表中数据制作较为形象的统计图。（2）根据你画的统计图，你能得到哪些信息？（至少从三个侧面说出信息）
8、（6分）任意写一个三位数A，百位数字比个位数字大2，交换百位数字与个位数字得到一个新数B，令C1=A－B，交换C1的百位数字与个位数字得另一新数C2，再计算C1+C2，此时结果应是多少？并说明你的理由。
9、帮卡当出主意（5分）
概率论起源于赌博，据传意大利的业余数学家卡当就曾热衷于赌博，试图研究赌博不输的方法。
卡当曾参加过这样一次赌博：把两个骰子掷出去，以每个骰子朝上的点数之和作为赌的内容，那么你认为卡当把赌注下在几点最有利呢？并说明理由。