黄岩宁溪中学七年级（下）数学期末试题 2004.6
（满分120分，时间90分钟，命题：朱云洲）
班级 学号 姓名_________评分
一、 选择题（每小题3分，共30分）
1、下列各题中的数据，精确的是（ ）
A、小颖班上共有56位同学； B、我国人口总数约为13亿；
C、珠玛朗玛峰的海拔高度为8848米；
D、我们数学教科书封面的长为21厘米。
2、下面每组数分别是三根小木棒的长度, 它们能摆成三角形的是（ ）
A、12cm, 3cm, 6cm； B、8cm, 16cm, 8cm；
C、6cm, 6cm, 13cm； D、2cm, 3cm, 4cm。
3、下面的运算正确的是（ ）
A.、(
；
B、 
；
C、(
； D、
.
4、在一个不透明的袋子里放入8个红球，2个白球，小明随意地摸出一球，
这个球是白球的概率为（ ）
A、0.2； B、0.25； C、0.4； D、0.8
5、一个角的度数是40°，那么它的余角的补角度数是（ ）．
A、130°； B、140°； C．50°； D．90°
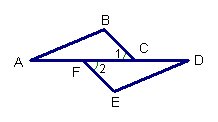6、如图，已知：
，
，下列
条件中能使ΔABC≌ΔDEF的是（ ）
A、
； B、
；
C、
； D、
7、下列图形中对称轴条数最多的是（ ）
A、线段 ； B、等边三角形 ； C、正方形 ； D、钝角
8、下列说法中错误的是（ ）
A、三角形的中线、角平分线、高线都是线段；
B、任意三角形的三内角和都是1800；
C、三角形按角分可分为锐角三角形、直角三角形和等边三角形；
D、直角三角形的两锐角互余。
9、一种商品售价为120元，由于购买的人多，商家便提价25％销售，
但提价后，商品滞销，商家只好再降价x％，使商品恢复到原价，
那么x％＝（ ）
Ａ、25 Ｂ、20 Ｃ、25％ Ｄ、20％
10、小明一出校门先加速行驶，然后匀速行驶一段后，在距家门不远的地方开始减速，最后停下，下面的图（ ）可以近似地刻画出他在这一过程中的时间与速度的变化情况。
 |  |
A 速度
B 速度
C 速度
D 速度
 | |||||||||
 |  | ||||||||
 |  | ||||||||
时间
时间
时间
时间
 |  |
二、填空题（每小题3分，共30分）
11、计算
12、有一种原子的直径约为0.米，它可以用科学计数法表示为___________米。
13、已知等腰三角形一个内角的度数为70°，则它的其余两个内角的度数分别是_____ _ 。
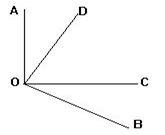
14、如图∠AOB＝125°，AO⊥OC，BO⊥OD则∠COD＝___________．
 |  |
15、如图：已知△ABC≌△EBF，AB⊥CE，ED⊥AC，若AB=5cm,BC=3cm，
则AF= 。
16、已知等腰三角形的一边等于10㎝另一边等于5㎝，则它的周长为_____。
17、若4a
＋2ka +9是一个完全平方式，则k 等于 。
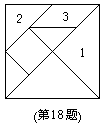
18、一只蚂蚁自由自在地在用七巧板拼成的正方形
中爬来爬去（每块七巧板的表面完全相同）它
最终停留在1号七巧板上的概率 。
19、如图是用四张相同的长方形纸片拼成的图形，请 利用图中空白部分的面积的不同表示方法写出
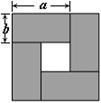一个 关于a、b的恒等式
.
20、若
三、解答题
21、（6分）20032 —2002×2004（利用公式计算） (第19题图)
22、（10分）计算：（1）(a-1)(a2+a+1) （2）
23、（8分）已知:2x-10+(y+2)2=0,求xy的值.
 |
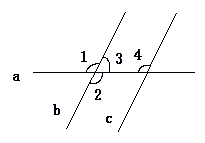24、（8分）如图，∠1＋∠2＝284°，b∥c，
求∠3，∠4的度数。
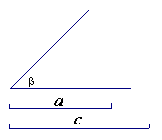
25、（8分）已知：线段
、
和∠β（如图），利用直尺和圆规作ΔABC，
使BC=，AB=，∠ABC=∠β。（不写作法，保留作图痕迹）。
26、（8分）图为一位旅行者在早晨8时从城市出发到郊外所走的路程S（单位：千米）与时间t（单位：时）的变量关系的图象。根据图象回答问题：
（1）在这个变化过程中，自变量
是____，因变量是______。
（2）9时，10时，12时所走的路程
分别是多少？
（3）他休息了多长时间？
（4）他从休息后直至到达目的地这
段时间的平均速度是多少？
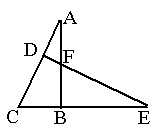
27、（12分）在直角三角形ABC中，BC=6，AC=8，点D在线段AC上
从C向A运动。若设CD=x,⊿ABD的面积为y.
（1）、请写出y与x的关系式；
（2）、当x为何值时，y有最大值，最大值是多少？此时点
D在什么位置？
（3）、当⊿ABD的面积是⊿ABC的面积的一半时，
点D在什么位置？
