初一数学2001-2002第二学期期中复习卷
一、判断题:
1、二元一次方程![]() 有无数多个解 ( )
有无数多个解 ( )
2、若![]() ( )
( )
3、若![]() ( )
( )
4、不等式组![]() ( )
( )
5、若方程组![]() ( )
( )
6、不等式![]() ( )
( )
7、若![]() ( )
( )
8、方程![]() 是二元一次方程 ( )
是二元一次方程 ( )
9、不等式组![]() 的解集是空集 ( )
的解集是空集 ( )
10、若![]() ( )
( )
11、若![]() ( )
( )
12、若![]() ( )
( )
13、经过两点有一条直线,并且只有一条直线 ( )
14、线段是两个端点之间的部分 ( )
15、把一个角分成两个角的射线,叫做这个角的平分线 ( )
16、![]() 的角 ( )
的角 ( )
17、如果![]() ( )
( )
18、如果一个角的补角是这个角的3倍,则这个角为![]() ( )
( )
19、一个钝角与一个锐角一定是互为补角 ( )
20、两个锐角不一定互余 ( )
21、若两个角![]() 互余 ( )
互余 ( )
22、若![]() ( )
( )
23、在几何中,“连结”与“联接”的意义是相同的 ( )
24、在平面内有四个点A、B、C、D,则一定有AB+BC+CD+DA>2AC ( )
二、选择题:
25、下列方程中,是二元一次方程的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
26、方程![]() 的非负整数解有( )
的非负整数解有( )
A、1个 B、2个 C、3个 D、4个
27、如果m<n,那么下列不等式中成立的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
28、下列结论中正确的是( )
A、![]() B、若
B、若![]()
C、若![]() D、
D、![]()
29、下列结论中正确的是( )
A、![]() B、
B、![]()
C、![]() ` D、
` D、![]()
30、若![]() ,则下面不等式成立的是( )
,则下面不等式成立的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
31、若![]() 成立,那么( )
成立,那么( )
A、c>0 B、![]() C、c<0 D、
C、c<0 D、![]()
32、不等式![]() 的解集为( )
的解集为( )
A、![]() B、
B、![]() C、
C、![]() D、以上答案都不对
D、以上答案都不对
33、若二元一次方程![]() 有公共解,则m的取值为
有公共解,则m的取值为
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
34、若![]() ,那么下列式子中正确的是( )
,那么下列式子中正确的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
35、若![]() ,则a的取值范围是( )
,则a的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
36、方程![]() 的整数解共有( )
的整数解共有( )
A、4组 B、5组 C、6组 D、无数多组
37、下列说法中,错误的是( )
A、经过两点有且只有一条直线 B、两条直线相交,只有一个交点
C、延长线段AB到C,使![]() D、延长线段AB到C,使AC=BC
D、延长线段AB到C,使AC=BC
38、下列说法中,正确的是( )
A、一个角的余角是锐角 B、一个角的补角是钝角
C、两个锐角的和是钝角 D、锐角与钝角的和是平角
39、已知点C是线段AB上的一点,则下列条件中不能判断点C 是线段AB中点的是
( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
40、已知平面上有四个点,过其中任意两个点画一条直线,那么可以画直线( )
A、6条 B、4条 C、1条 D、以上都有可能
41、如果A、B、C、D、四点依次在一条直线上,并且AB:BC:AD=2:3:9,E为CD的中点,那么AB:AE=( )
A、4:19 B、2:5 C、2:7 D、2:9
42、在6点10分的时候,钟面上时针与分针所成的角为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
三、填空:
43、方程![]() ,用x的代数式表示y,则y=______________
,用x的代数式表示y,则y=______________
44、当a________时,方程组![]() 无解;
无解;
45、若![]() _______________
_______________
46、若![]() ________________
________________
47、在方程组![]() 的取值范围是____________________
的取值范围是____________________
48、不管是取![]() 总是能成立,那么当
总是能成立,那么当![]() ______________。
______________。
49、若![]() _______
_______![]() ;
;
50、若![]() _____;
_____;
51、已知关于x,y的方程组![]() 的解中x与y的值相等,则k=_______;
的解中x与y的值相等,则k=_______;
52、若![]() 的公共部分为__________;
的公共部分为__________;
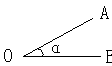 53、如图所示,请用三种不同的方法表示这个角:_______________________;
53、如图所示,请用三种不同的方法表示这个角:_______________________;
54、已知线段a,画线段AB = a,延长AB至C,使AC=2a,在AB的反向延长线上取一点E,使![]() ,那么CE= _________a, AC=_________CE, CE=_________BC;
,那么CE= _________a, AC=_________CE, CE=_________BC;
55、已知线段AB,延长AB至C,使BC=AB,在AB的反向延长线上截取AD=AC,则
DB:AB=___________, CD:BD=____________;
56、20点20分的时刻,时钟的时针与分针的夹角是_________度;
 57、
57、![]() ________;
________;
58、平面内有五条直线,它们两两相交,则得到的交点的个数为_________个;
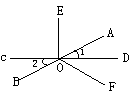
59、如图所示,已知直线AB、CD相交于点O,![]()
![]()
![]() ______度,
______度,![]() ___________度。
___________度。
60、已知![]() _____°_____’______’’;
_____°_____’______’’;
四、解下列方程组:
![]()
![]() (1)
(1)
61、用代入消元法解方程组
![]() (2)
(2)
![]()
![]() (1)
(1)
62、用加减消元法解方程组
![]() (2)
(2)
![]()
![]() (1)
(1)
63、解方程组 ![]() (2)
(2)
![]() (3)
(3)
五、解下列一元一次不等式(组);并把解集在数轴上表示出来;
64、![]() ;
;
![]()
![]() (1)
(1)
65、
![]() (2)
(2)
六、解答题;
66、已知关于x的不等式![]() ,求a的值。
,求a的值。
67、已知![]() 的取值范围;
的取值范围;
68、某校有住宿生若干人,住若干间宿舍,如果每间宿舍住4人,那么还余下18个人没有宿舍住;如果每间宿舍住6人,那么有一间宿舍没有住满,求该校住宿生的人数和宿舍的间数;
69、某人要在预定的时间内由甲地到达乙地,如果他每小时行35千米,那么他就要迟到2个小时;如果他每小时行50千米,那么他就可以提前1小时到达,求甲、乙两地之间的路程和预定的时间;
70、一列火车通过167千长的铁路需要20秒,而这列火车通过506米长的隧道需要50秒钟,求这列火车的长度和它行驶的速度;
71、一个圆形工件,圆心是O,半径是48mm,点C是直径AB上的一个点,CO=28mm,求点C与圆上各个点之间的最大距离和最小距离的差;
73、已知线段AB,延长AB到C,使BC等于AB的2倍,如果线段AB=60厘米,AB的中点是D,E、F两点在线段BC上,且BE:EF:FC=1:2:5,求线段DF和CF的长;
74、如图所示,![]() 求线段EF的长;
求线段EF的长;
![]()
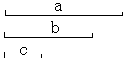 75、如图所示,已知线段a,b,c(a>b),画一条线段使它等于
75、如图所示,已知线段a,b,c(a>b),画一条线段使它等于![]() (要求:画出图形、不与画法、保留痕迹,说明结果)
(要求:画出图形、不与画法、保留痕迹,说明结果)
【参考答案】
一、
1、√ 2、√ 3、× 4、× 5、√
6、√ 7、√ 8、× 9、× 10、
11、× 12、√ 13、√ 14、× 15、
16、√ 17、× 18、× 19、× 20、√
21、× 22、√ 23、× 24、×(有可能是![]() )
)
二
25、C 26、C 27、C 28、A 29、D
30、C 31、C 32、D 33、C
34、C 35、D;(本题需要分①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 这四种情况进行讨论);
这四种情况进行讨论);
36、C;(可将方程化为![]() =
=![]()
![]() 可以
可以![]() 共计六个值);
共计六个值);
37、D 38、A 39、A 40、D
41、A 42、B
三、
43、![]() 44、=-4 45、7:4 46、
44、=-4 45、7:4 46、![]() 47、
47、![]()
48、45 49、> 50、4,-4或-2 51、11 52、c<x<b
53、![]() 54、3,
54、3,![]() ,3; 55、3:1,4;3
,3; 55、3:1,4;3
56、![]() 57、
57、![]() 58、一或Z或六或八或十;
58、一或Z或六或八或十;
59、130 100; 60、56,55,55;
四、
61、![]() 62、
62、![]() 63、
63、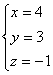
五、64、![]() 65、
65、![]()
六、66、![]() 67、
67、![]()
68、设宿舍x间,则住宿生的人数为(![]() )人
)人
![]()
解之得 ![]()
![]() 人数为58或62
人数为58或62
69、350千米,8小时
70、11.3米/秒 长为59米
71、设这个角为![]()
解之得x=40,![]()
72、最大距离为![]()
最小距离为![]()
![]() (mm)
(mm)
73、如图,每一小份为![]() 厘米;
厘米;
![]()
74、![]()
75、(略)