四边形单元测试题Ⅱ
一、选择题(每小题3分,共30分)
1、能够判定一个四边形是平行四边形的条件是 （ ）
A、一组对角相等 B、两条对角线互相平分
C、两条对角线互相垂直 D、一对邻角的和为180°
2、
中，
的值可以是（ ）
A．1：2：3：4 B．1：2：2：1 C．2：2：1：1 D．2：1：2：1
3、对角线互相垂直平分的四边形是 （ ）
A、平行四边形 B、矩形 C、菱形 D、梯形
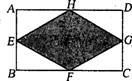
4、已知：如图，在矩形ABCD中，E、F、G、H分别为边AB、BC、CD、DA的中点．若AB＝2，AD＝4，则图中阴影部分的面积为 ( )
A．8 B．6 C．4 D．3
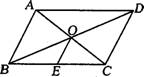
5、如图，□ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3 cm，则AB的长为 ( )
A．3 cm B．6 cm C．9 cm D．12 cm
6、如图,□ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( )
A.18° B.36° C.72° D.108°
7、下列四个命题中，假命题是（ ）．
A 等腰梯形的两条对角线相等
B 顺次连结四边形的各边中点所得的四边形是平行四边形
C 菱形的对角线平分一组对角
D 两条对角线互相垂直且相等的四边形是正方形
8、等腰梯形的腰长为13cm，两底差为10cm，则高为 （ ）
A、
cm
B、12cm C、69cm D、144cm
9、已知四边形ABCD的对角线相交于O，给出下列 5个条件①AB∥CD ②AD∥BC③AB=CD ④∠BAD=∠DCB，从以上4个条件中任选 2个条件为一组，能推出四边形ABCD为平行四边形的有（ ）
A 6组 B.5组 C.4组 D.3组
10、某校计划修建一座既是中心对称图形又是轴对称图形的花坛，从学生中征集到设计方案有等腰三角形、正三角形、等腰梯形、菱形等四种图案，你认为符合条件的是（ ）．
A．等腰三角形 B．正三角形 C．等腰梯形 D．菱形
二.填空题: (每小题3分,共24分)
1．在□ABCD中，∠A+∠C=270°，则∠B=______，∠C=______.
2．平行四边形的周长等于56 cm，两邻边长的比为3∶1，那么这个平行四边形较长的边
长为_______.
3．平行四边形ABCD，加一个条件__________________，它就是菱形．
4．如图，长方形ABCD是篮球场地的简图，长是28m，宽是15m，则它的对角线长约为________m．（精确到1m）
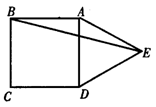5 如图，在正方形ABCD的外侧，作等边△ADE，则∠AEB=_______．
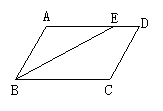
6.如图，在梯形ABCD中，AD∥BC，DE∥AB，△DEC的周长为10cm，BE=5cm，则该梯形的周长为 。
7．若菱形的周长为24 cm，一个内角为60°，则菱形的面积为______ cm2。
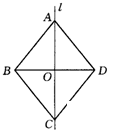8．如图，l是四形形ABCD的对称轴，如果AD∥BC，有下列结论：①AB∥CD ②AB＝BC ③AB⊥BC ④AO＝OC其中正确的结论是
。（把你认为正确的结论的序号都填上）
三.解答题: (共66分)
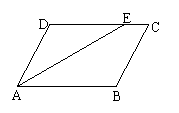1.（6分）已知：在□ABCD中，∠A的角平分线交CD于E，若
，AB的长为8，求BC的长。
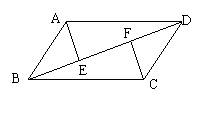
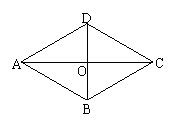2.（7分）、如图，在菱形ABCD中，AB=BD=5，
求：（1）∠BAC的度数；（2）求AC的长。
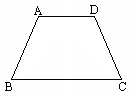
3. （7分）、已知：如图，梯形ABCD中，CD//AB，
，
．
求证：AD=AB—DC．
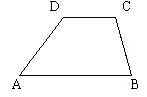
4．（7分）、已知：如图，在四边形ABCD中，∠B=∠C，AB与CD不平行，且AB=CD．求证：四边形ABCD是等腰梯形．
5. （7分）、如图，平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F，
求证：∠BAE＝∠DCF。
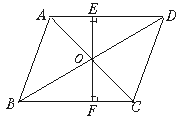
6. （7分）、如图，在
ABCD中，O是对角线AC和BD的交点，OE⊥AD于E，OF⊥BC于F.
求证：OE=OF.
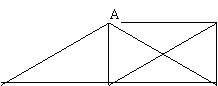
7、（7分）如图， 四边形ABCD是矩形，过A作AE∥BD交CB的延长线于点E，猜想△ACE是怎样的三角形，并证明你的猜想。
 | |||||||
| |||||||
|
| ||||||
| |||||||
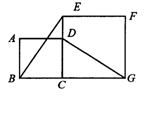
8.（8分）如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接BE、DG.
观察猜想BE与DG之间的大小关系，并证明你的结论；
 |
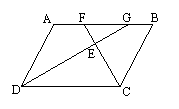
9. （10分）如图，已知四边形ABCD是平行四边形，∠BCD的平分线CF交边AB于F,∠ADC的平分线DG交边AB于G.
（1）求证：AF=GB;
（2）请你在已知条件的基础上再添加一个条件，使得△EFG为等腰三角形，并说明理由。
 |