八年级数学四边形试卷
2008、6、4
班级 姓名 座号 评分
一、选择题。（每小题3分，共30分．）
1、下列哪组条件能判别四边形ABCD是平行四边形？（ ）
A、AB∥CD，AD＝BC B、AB＝CD，AD＝BC
C、∠A＝∠B，∠C＝∠D D、AB＝AD，CB＝CD
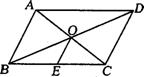2、如图，□ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3 cm，则AB的长为 ( )
A．3 cm B．6 cm C．9 cm D．12 cm
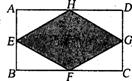3、已知：如图，在矩形ABCD中，E、F、G、H分别为边AB、BC、CD、DA的中点．若AB＝2，AD＝4，则图中阴影部分的面积为 ( )
A．8 B．6 C．4 D．3
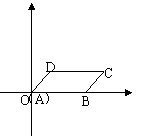
4、如图，在平面直角坐标系中，□ABCD的顶点A、B、D的坐标分别是（0，0），（5，0）（2，3），则顶点C的坐标是（ ）
A．（3，7） B.（5，3） C.（7，3） D.（8，2）
5、如图是用4个相同的小矩形与1个小正方形镶嵌而成的正方形图案．已知该图案的面积为49，小正方形的面积为4，若用x、y表示小矩形的两边长(x＞y)，请观察图案，指出以下关系式中不正确的是 ( )
A．
B．
C．
D．
6、□ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( )
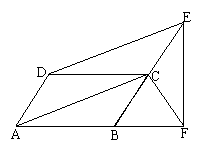
A.18° B.36° C.72° D.108°
7、平行四边行的两条对角线把它分成全等三角形的对数是（ ）
A.2 B.4 C.6 D.8
8、用两块完全相同的直角三角形拼下列图形：①平行四边形 ②矩形 ③菱形 ④正方形 ⑤等腰三角形 ⑥等边三角形，一定能拼成的图形是（ ）
A、①④⑤ B、②⑤⑥ C、①②③ D、①②⑤
9、等腰梯形的腰长为13cm，两底差为10cm，则高为 （ ）
A、
cm
B、12cm C、69cm D、144cm
10、小明和小亮在做一道习题，若四边形ABCD是平行四边形，请补充条件 ，使得四边形ABCD是菱形。小明补充的条件是AB=BC；小亮补充的条件是AC=BD，你认为下列说法正确的是（ ）
A、小明、小亮都正确 B、小明正确，小亮错误
C、小明错误，小亮正确 D、小明、小亮都错误
二、填空题（共10小题，每小题3分，共30分）
11、如图，若四边形ABCD是平行四边形，请补充条件 (写一个即可)，使四边形ABCD是矩形．
|
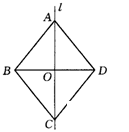
13、如图，l是四形形ABCD的对称轴，如果AD∥BC，有下列结论：
①AB∥CD ②AB＝BC ③AB⊥BC ④AO＝OC
其中正确的结论是 。（把你认为正确的结论的序号都填上）
 | |||
| |||
（第11题图） （第12题图） （第13题图）
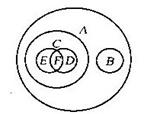14、如图为四边形、平行四边形、矩形、正方形菱形、梯形集合示意图，请将字母所代表的图形分别填入下表：
| A | B | C | D | E | F |
15、在
中，两邻边的差为4cm，周长为32cm，则两邻边长分别为________．
16、已知菱形两条对角线的长分别为5cm和8cm，则这个菱形的面积是______cm．
17、对角线长为10 cm的正方形的边长是______cm，
面积是______ cm2。
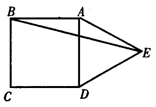
18、 如图，在正方形ABCD的外侧，作等边△ADE，
则∠AEB=_______．
19、如图，在梯形ABCD中，AD∥BC，DE∥AB，△DEC的周长为10cm，BE=5cm，则该梯形的周长为 。
20、若菱形的周长为24 cm，一个内角为60°，则菱形的面积为______ cm2。
三、解答题。（每小题10分，共40分)
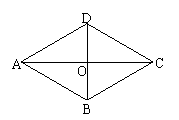21、如图，在菱形ABCD中，AB=BD=5，
求：（1）∠BAC的度数；（2）求AC的长。
22、已知：如图，梯形ABCD中，AD∥BC，∠B=60°，∠C=30°，AD=2，BC=8。
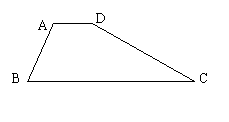求：梯形两腰AB、CD的长。
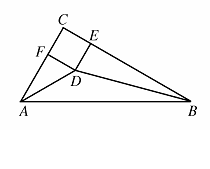
23、如图，在△ABC中，∠C＝90°，∠A、∠B的平分线交于点D，DE⊥BC于点E，DF⊥AC于点F.求证： 四边形CFDE是正方形．
24、已知：如图，四边形ABCD是平行四边形，DE//AC，交BC的延长线于点E，EF⊥AB于点F，求证：AD=CF。
