八年级数学春季学期段考试题
八年级数学
（考试时间：120分钟，卷面总分：120分）
| 题 号 | 一 | 二 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 总 分 |
| 赋 分 | 30 | 24 | 6 | 8 | 6 | 8 | 8 | 8 | 10 | 12 | 120 |
| 得 分 |
一、填空题（每小题3分，共30分）
1.当x 时，分式
没有意义；
2.式子①
②
③
④
中，是分式的有 (填序号即可)；
3．自从扫描隧道显微镜发明后，世界上便诞生了一门新学科，这就是“纳米技术”，已知52个纳米的长度为0.米,用科学记数法表示 这个数为 米.
4. 若函数y=
的图象有一个点是A（2，m），则m的值是 。
5.木工周师傅做一个长方形桌面，测量得到桌面的长为80cm，宽为60cm，对角线为120cm，这个桌面 (填”合格”或”不合格”)。
6.写出一个反比例函数，使得它的图象在一、三象限内，这个反比例的
解析式是 ；
7. 等腰△ABC的底边BC为16，底边上的高AD为6，则腰长AB的长为 。
8.若关于x的方程
的解是x=5，则a=
；
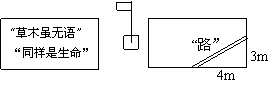
9.如图，是某中学东操场旗杆两
侧的花园示意图，有少部分同学为
了走近路在花园中踩出了一条“路”，
请你帮他们算一算， 仅仅为了少走 米，而贱踏了“无语的生命”.
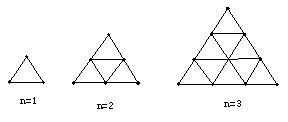10.如图所示,用火柴杆摆出一系
列三角形图案,按这种方式摆下
去,当摆到19层(n=19)时,需要
根火柴?
二、选择题（每小题3分，共24分）
1.下列函数中，是反比例函数的是（ ）
A. B.
C. D.
2.△ABC的三条边长分别是
、
、
，则下列各式成立的是（ ）
A．
B.
C.
D.
3.若方程
有增根，则m的值是（ ）
A．3 B．4 C．－3 D．1
4.如果把分式
中的x、y都扩大10倍，则分式的值是（ ）
A、扩大100倍 B、扩大10倍 C、不变 D、缩小到原来的
5.下面各式，计算正确的是（ ）
 |
A. B. C. D.
6.当路程
一定时，速度
与时间
之间的函数关系是（ ）
A一次函数 B. 二次函数 C. 正比例函数 D. 反比例函数
7.在△ABC中，AB=12cm， BC=16cm， AC=20cm， 则△ABC的面积是( )
A、96cm2 B、120cm2 C、160cm2 D、200cm2
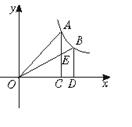
8.如图，过反比例函数y=
(x＞0)图象上任意两点A、B分别作x轴
的垂线，垂足分别为C、D，连结OA、OB，设AC与OB的交点为E，
△AOE与梯形ECDB的面积分别为S1、S2，比较它们的大小，可得（ ）
A.S1＞S2 B.S1＜S2
C.S1=S2 D.S1、S2的大小关系不能确定
三、解答题（共66分）
19.（6分）计算：
20.（8分）解分式方程：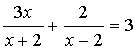
。
21. （6分）下面是数学课堂的一个学习片段, 阅读后, 请回答下面的问题:
学习勾股定理有关内容后, 张老师请同学们交流讨论这样一个问题
“已知直角三角形ABC的两边长分别为3和4, 请你求出第三边.”
同学们经片刻的思考与交流后, 李明同学举手说: “第三边长是5”;王华同学说: “第三边长是
.” 还有一些同学也提出了不同的看法……
（1）假如你也在课堂上, 你的意见如何? 为什么?
（2）通过上面数学问题的讨论, 你有什么感受? (用一句话表示)
22．（8分）
先化简代数式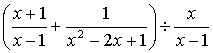
，然后选取一个使你喜欢的
的值代入求值.
23. 列方程解应用题：（8分）
八年级学生去距学校10km的小山值树，一部分学生骑自行车先走，20分钟后，其余学生坐汽车出发，结果他们同时到达，已知汽车的速度是骑车同学的3倍，求骑车同学的速度？
24.（8分）反比例函数
的图象经过点
.
（1）求这个函数的解析式；
（2）请判断点
是否在这个反比例函数的图象上，并说明理由.
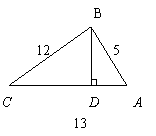
25.（10分）如图，三个村庄A、B、C之间的距离分别为AB=5km,BC=12km,AC=13km.要从B修一条公路BD直达AC.已知公路的造价为26000元/km，求修这条公路的最低造价是多少？
 |
26.（12分）、已知甲、乙两站的路程是312 km,一列列车从甲站开往乙站，设列车的平均速度为
km/h，所需时间为
h。
（1）试写出关于的函数关系式；
（2）一列列车从甲站到乙站需要4 h，求这列列车从甲站到乙站的平均速度是多少？
（3）2006年全国铁路第六次大提速，提速后，（2）中的这列列车的速度提高了26 km/h，问提速后从甲站到乙站需要几个小时？