第二学期八年级数学期末检测试卷
（考试时间100分钟，满分100分+20分）
一、 填空题（本大题共12小题，每小题3分，满分36分）
1. 直线y=4x–1与直线y=4x+2的位置关系是__________.
2.
一次函数
的图象与
轴的交点为__________.
3.
一次函数
中，
随着
的增大而___________.
4.
方程
的根是
.
5.
如果关于的方程
没有实数根，那么
的取值范围是__________.
6.
一元二次方程
的两根的积是_________.
7.
二次函数
的图象的对称轴是_______________.
8. 点A(2,–3)与B(–3, 9)之间的距离AB=_____________.
9. 通过两定点A、B的圆的圆心的轨迹是_____________________.
10. 在△ABC中，点D在BC边上，BD=4，CD=6，那么S△ABD：S△ACD=___________.
11. 在四边形ABCD中, AB=CD, 要使四边形ABCD是平行四边形, 只须添加一个条件, 这个条件可以是______________(只要填写一种情况).
12. 在Rt△ABC中，∠C=90º，AB=5，AC=4，△ABC绕点A旋转后点C落在AB边上，点B落在点B’，那么BB’的长为_____________.
二、选择题（本大题共4小题，每小题3分，满分12分）
【每小题只有一个正确答案,将代号填入括号内】
13.
关于x的一元二次方程
的根的情况是……………………（ ）
（A）没有实数根; （B）有两个相等的实数根;
（C）有两个不相等的实数根; （D）不能确定的．
14. 二次函数
的图象不经过………………………………………………( )
(A) 第一象限； （B）第二象限； （C）第三象限； （D）第四象限．
15. 以下列长度的三条线段为边不能组成直角三角形的是………………………（ ）
（A）2、3、4； （B）2、3、
；
（C）3、4、5； （D）3、4、
.
16. 下列命题中，真命题是…………………………………………………………（ ）
（A） 对角线互相垂直且相等的四边形是菱形；
（B） 对角线互相垂直且相等的四边形是矩形；
（C） 对角线互相平分且相等的四边形是菱形；
（D） 对角线互相平分且相等的四边形是矩形.
三、（本大题共4小题，每小题6分，满分24分）
17.
解关于x的方程: (1) 
; (2) 
.
18. 二次函数
的图象经过点（0,–6）、（3，0），求这个二次函数的解析式，并用配方法求它的图象的顶点坐标.
19.
已知二次项系数为1的一元二次方程的两个根为
、
，且满足
, 求这个一元二次方程.
20. 如图，矩形ABCD中，AC与BD交于O点，BE⊥AC，CF⊥BD, 垂足分别为E、F．
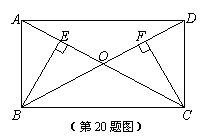求证: BE=CF．
四、（本大题共4小题，每小题7分，满分28分）
21.
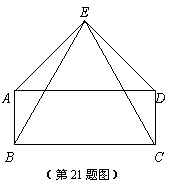如图，四边形ABCD是矩形，△EAD是等腰直角三角形，△EBC是等边三角形. 已知AE=DE=2，求AB的长.
22.
如图，在一张三角形的纸片ABC中，已知∠C=90º，∠A=30º, AB=10. 将△ABC纸片折叠后使其中的两个顶点能够互相重合，请画出与说明折痕的各种可能的位置，并求出每条折痕的长.
23.
分别写出一个一次函数和一个二次函数使它们都满足以下的条件：当自变量的值取–3时，函数的值为正数，而当的值为–1、2时，的值均为负数. 并分别说明你所写出的函数符合上述条件.
24.
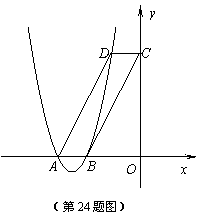
如图，二次函数
的图象与轴的负半轴相交于A、B两点（点A在左侧），一次函数
的图象经过点B，与轴相交于点C．
（1）
求A、B两点的坐标（可用的代数式表示）；
（2）
如果□ABCD的顶点D在上述二次函数的图象上，求的值．
五、附加题（本大题供学有余力学生选做，共2小题，每小题10分，满分20分）
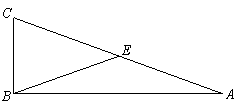
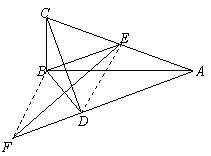
25. 如图，△ABC中，∠ABC=90°, E为AC的中点．
操作：过点C作BE的垂线, 过点A作BE的平行线，两直线相交于点D，在AD的延长线上截取DF=BE．连结EF、BD.
(1) 试判断EF与BD之间具有怎样的关系? 并证明你所得的结论．
（2）如果AF=13，CD=6，求AC的长.
|
26.
已知直角梯形ABCD的腰AB在轴的正半轴上，CD在第一象限，AD//BC，AD⊥轴，E、F分别是AB、CD的中点．
(1)
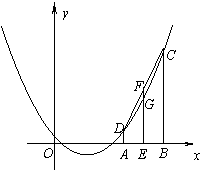
如图1，抛物线
经过C、D两点，且与EF相交于点G，如果点A、B的横坐标分别为1、3，求线段FG的长；
(2)
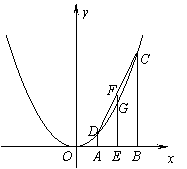
如图2，抛物线
（
经过C、D两点，且与EF相交于点G，如果点A、B的横坐标分别为
、
，求线段FG的长．
|
|
2005学年度第二学期八年级数学期末检测试卷参考答案及评分意见 2006.6
一、填空题（本题共12小题，每小题3分，满分36分）
1．
互相平行； 2．（2，0）； 3．减小； 4．
； 5．
； 6．–
；
7．轴； 8．13； 9．AB的垂直平分线； 10．2∶3；
11．AB//CD、AD=BC、∠B+∠C=180º等； 12．
．
二、选择题（本大题共4小题，每小题3分，满分12分）
13．C； 14．C； 15．A； 16．D．
三、（本大题共4小题，每小题6分，满分24分）
17．解：（1）
…（1分）=
…（1分）=
．……（1分）
（2）
……（1分） 
………（1分）
……………………………………………………………（1分）
18．解：由题意得
…………（1分）解得
…………（1分）
∴这个二次函数的解析式是
．………………（1分）
…（1分） =2
．…（1分）
∴它的图象的顶点坐标是（1，–8）．………………（1分）
19．解：∵
，∴
，（2分）
∴
，（2分）
∴这个一元二次方程为
，或
（2分）
20．证明：∵四边形ABCD为矩形，∴AC=BD，（1分）OB=
．（1分）∴OB=OC．…（1分）∵BE⊥AC，CF⊥BD，∴∠BEO=∠CFO=90º．…（1分）
又∵∠BOE=∠COF，∴△BOE≌△COF．…（1分）∴BE=CF．…（1分）
四、（本大题共4小题，每小题7分，满分28分）
21．解：过点E作EF⊥BC，交AD于G，垂足为F． …………………（1分）
∵四边形ABCD是矩形，∴AD //BC，∴EG⊥AD．…………………（1分）
∵△EAC是等腰直角三角形，EA=ED=2，
∴AG=GD，AD=
． ………………（1分）
∴EG=
．……………………………………………………（1分）
∵EB=EC=BC=AD=2，∴BF=
，………………………（1分）
∴EF=
．…………………………………（1分）
∴AB=GF=EF–EG=
．………………………………………（1分）
22．解：折痕可能位置为△ABC的中位线DE、DF及AB边的垂直平分线与AC的交点G与AB的中点D之间的线段（只要说明中点、垂直）（图形+说明每条1分）
在Rt△ABC中，∵∠C=90º，∠A=30º, AB=10，
∴BC=5，AC=
…（1分）
DE=
，(1分)DF=
．(1分)
设DG=，∵DG⊥AD，∴AC=
，
，DG=
．……（1分）
23．解：一次函数解析式可以是
等．………………（2分）
∵当
时，
；当
时，
；当
时，
．
∴符合条件．（2分）
二次函数解析式可以是
等．………………（2分）
∵当时，
；当时，；当时，．
∴符合条件．…………………………（1分）
24．解：（1）当
时，
，
．…（1分）∴A（
，0），B（
，0）．…（1分）
（2）∵一次函数的图象经过点B，∴
，
∴
．…………（1分）∴点C（0，
）．………………（1分）
∵四边形ABCD是平行四边形,∴CD//AB,CD=AB=4,∴D（–4,）.…（1分）
∵点D在二次函数的图象上,∴
,
,
.………(1分) 其中
不符合题意, ∴的值为8. ……（1分）
五、附加题（本大题供学有余力学生选做，共2小题，每小题10分，满分20分）
25．解：（图形1分）如图,（1）EF与BD互相垂直平分．…（1分）
证明如下：连结DE、BF，∵BE //DF，
∴四边形BEDF是平行四边形．……（1分）
∵CD⊥BE，∴CD⊥AD，
∵∠ABC=90º，E为AC的中点，
∴BE=DE=
，……………………（1分）
∴四边形BEDF是菱形．……………（1分）
∴EF与BD互相垂直平分．
（2）设DF=BE=，则AC=2，AD=AF–DF=13–．……………………（1分）
在Rt△ACD中，∵
，（1分）∴
．…（1分）
……（1分）∴AC=10．…………（1分）
26．解：∵EF是直角梯形ABCD的中位线，∴EF//AD//BC，EF=
．
∵AD⊥轴，∴EF⊥轴，BC⊥轴．……………………………………（1分）
（1）∵A、B的横坐标分别为1、3，∴点E的横坐标为2．
∴点D、G、E的横坐标分别为1、2、3. ……………………………………(1分)
∵抛物线经过点D、G、 C，∴AD=
，EG=3，BC=
．……（1分）
∴EF=
=
．………（1分）
∴FG=EF–EG=
．………（1分）
（2）∵A、B的横坐标分别为、，∴点E的横坐标为
．
∴点D、G、E的横坐标分别为、、. ……… (1分)
∵抛物线经过点D、G、C，
∴
, 
,
………（1分）
∴EF==
．………（2分）
∴FG=EF–EG=–
=
．…（1分）